[ベスト] 等しい 分数 の やり方 101709

分数にかっこがミックス！？ ラスボス感がありますね。笑 それでは、倒していきましょう。 まずは a を左辺に持っていくために 左辺と右辺をひっくり返します。 $$S=\frac{(ab)h}{2}$$ $$\frac{(ab)h}{2}=S$$ 分数を消すために両辺に2を掛けます。 $$\frac{(ab)h}{2}\times2=S\times2$$比の値の表し方は，分数，それとも小数なの 9 等しい比は，どうやってつくるの 10 12：9の比は，どうやってかんたんにするの 11 比をかんたんにするって，どんなことなの 12 2．1：0．9の比は，どうやってかんたんにするの 13 4．6 14問題 分数 の 約 分 の やり方 分数の約分のやり方と教え方のコツ｜時間短縮に便利なテクニックを紹介 管理人 9月 13, 18 / 12月 31, 19 分数の約分は公倍数の単元と密接な繋がりがあります。そのため公倍数が理解できていないと

通分 Instagram Posts Photos And Videos Picuki Com

等しい 分数 の やり方

等しい 分数 の やり方-教え方2 等しい分数のつくり方を教え、その後に約分・通分の意味と約分・通分のしかたを教えます。 図を見せるとわかりやすくなります。 上の図を見せて気がついたことを言わせましょう。 下の図のように、 分母と分子をそれぞれ2倍 すると、 同じ大きさの分数 になります。 同じように、 分母と分子を3倍 、 また6倍 にしても 同じ分数の大きさ になることに分母の積をみて前の数は、初項1公差2の等差数列より一般項は2n1、後ろの数はそれより2多いんだから2n1、だから一般項anは、 となります。 次に、分母の2数の差は、(2n1)(2n1)=2。 よって2で割って、 あとは和をドミノ倒しで求めるだけです。 できました。 ＜先 生＞ どうだろう。 消え方も鮮やかだけど、和の値も随分美しくまとまるものだね。

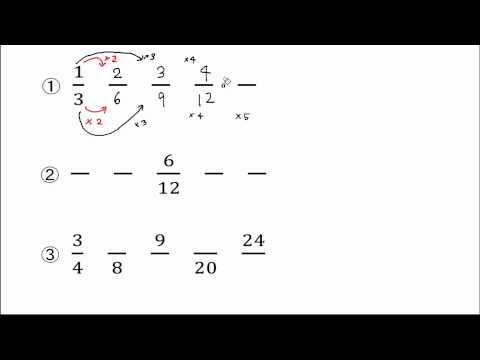
等しい分数をつくろう Youtube

比例式の解き方 比例式の性質 x y = 3 5 のように比が等しいことを表す式が 比例式 である。 比の性質から「等しい比の比の値は等しい」ので、 a b = m n なら a b = m n である。 両辺に bnをかけると an = bm となる。まず 1 1 区画の面積に着目しましょう。 全体で 1m2 1 m 2 の土地を縦に 3 3 分割、横に 5 5 分割しているので、 15 15 分割しているのがわかります。 この区画が縦横にそれぞれ 2 2 つ分並べられたのが今回求める土地です。 1 15 m2 1 15 m 2 が 2× 2 2 × 2 で並んでいるので、 2 ×2 15 ＝ 4 15(m2) 2 × 2 15 ＝ 4 15 ( m 2) となります。 つまり、次のように分母同士・分子同士で掛け算し目算法のやり方がよく分かりません😣😣 どなたか詳しく教えて頂けませんか？ ？ Clear どなたか詳しく教えて頂けませんか？ ？ 宜しくお願いします！ 🙇‍♂️ の n (の _全 NO5 一テ 千 No 中 O> N と x!

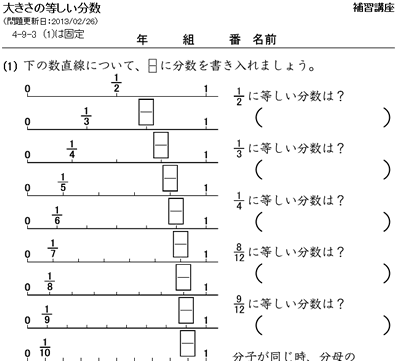
1大きさの等しい分数。 1 1／2と等しい大きさの分数を見つけましょう。 の中に数字を書き込みなさい。 ノートにも同じように書きなさい。 指名して答えさせる。 ④ 念のため，7／14の次はいくつになりますか。書きなさい。不定積分（まとめ2） 不定積分の漸化式 → 携帯版は別頁 == 分数関数の不定積分 == 《解説》 分数関数の不定積分については，次の流れに沿って処理すると分かりやすくなります． （1の詳細） 分子の次数が分母よりも大きいとき（又は等しいとき約分と通分 ICT教材eboard（イーボード） 教材を見てみる 使い方ガイド ログイン 教育現場でのご活用 1 等しい分数 2 等しい分数をつくろう 1 2

 分数 表し 方 分数 表し 方分数とは、ある数を 0 でない他の数で割った商を、横線の上（分子）に割られる数、横線の下（分母）に割る数を記して表したものです。 このページでは、分数の計算のやり方をまとめています。比についての自主学習ノートの例を、もう1つご紹介します。 前回、比の値を求めて、等しい比を見つける練習問題をやりました。 →比と比の値 「ab」という比で、比の値は「a÷b」で求めることができます大きさの等しい分数の 存在を認め，分数の意 味の理解を深めようと している。（ノート・発 表） 既習事項を手 がかりに課題 を解決しよう とするチャレ ンジ精神（ノ ート） 2 情報の収集 約分の意味とそのやり 方について理解する。 約分すると分数の大き

分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun

帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説

教え方1 箱を包んだリボンのそれぞれの長さを調べ、 1より大きいはしたの分数 を理解させます。 そして、 真分数 と 仮分数の意味 を教えます。 4本のリボンの長さを比べました。 ②の長さは、1mを 2つに等しく分けた1つ分 の長さのリボンです。 ③の長さは、 1mを3つに等しく分けた1つ分 の長さのリボンです。 ④の長さは、 1mを4つに等しく分けた1つ分 の長さの・ 等しい分数の作り方とその性質を理解す る。（1） 類推 比較 発言 ・ 異分母分数の大小や計算に ついて関心を持ち，取り組も うとしている。 関（発言・ノート） ・ 等しい分数の作り方を理解 している。 知（ノート） c 論理的思考 力 ( ・ワークとそれぞれ大きさが等しい分数を見つけ てノートに書きましょう。 1 3 ＝ 1 4 ＝ 分数は、分母がちがっていても、大きさの等しい分数 がたくさんあります。 / 上の数直線を見て、分子が1の分数を大きい順にノートに書きましょう。 1 2

算数 の記事一覧 塾の先生が作った本当に欲しいプリント 楽天ブログ

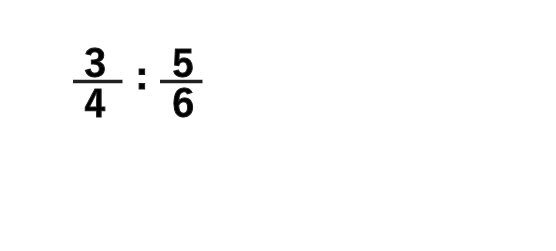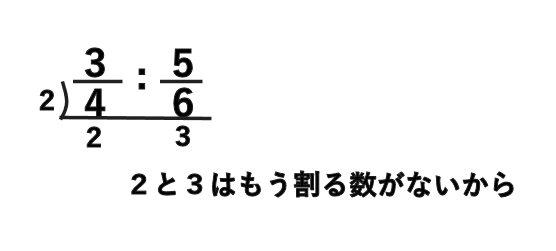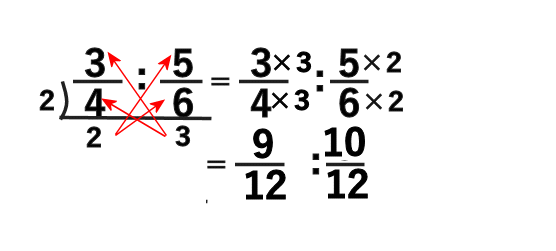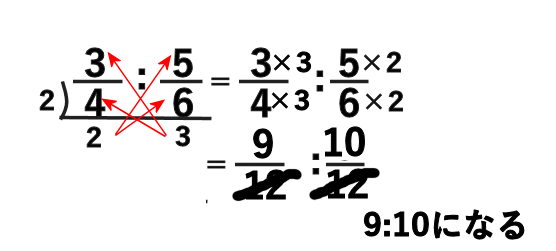
分数の比を簡単にする

分母がちがう分数のたし算／理解シート 大きさの等しい分数のつくり方を教えて 無断複製・転載・翻訳を禁ず GAKKEN B (大きさの等しい分数) Title 算数 Author VAIO Created Date PM小学5年生の算数 わり算と分数｜商分数／分数の第二義 練習問題プリント 分数にある2つの意味のうち、第一義 （ 1を3等分したものを2つ集めたもの＝ 2/3 ）は3年生で学習します。 このページのプリントでは、第二義 （ 2を3でわったもの＝ 2/3 ）つまり、わり算の商を表すための分数 (商の分数）を中心に、その表し方や計算方法を練習します。 （プリント10枚） 8時間目帯分数の足し算・引き算① ーーーーーーーーーーーーーーーーーーーーーーーーーーー 9時間目帯分数の足し算・引き算② 帯分数を、整数と分数に分けて計算する。このやり方を子ども達にはマスターして欲しいですよね。

5年 分数1 等しい分数 Youtube

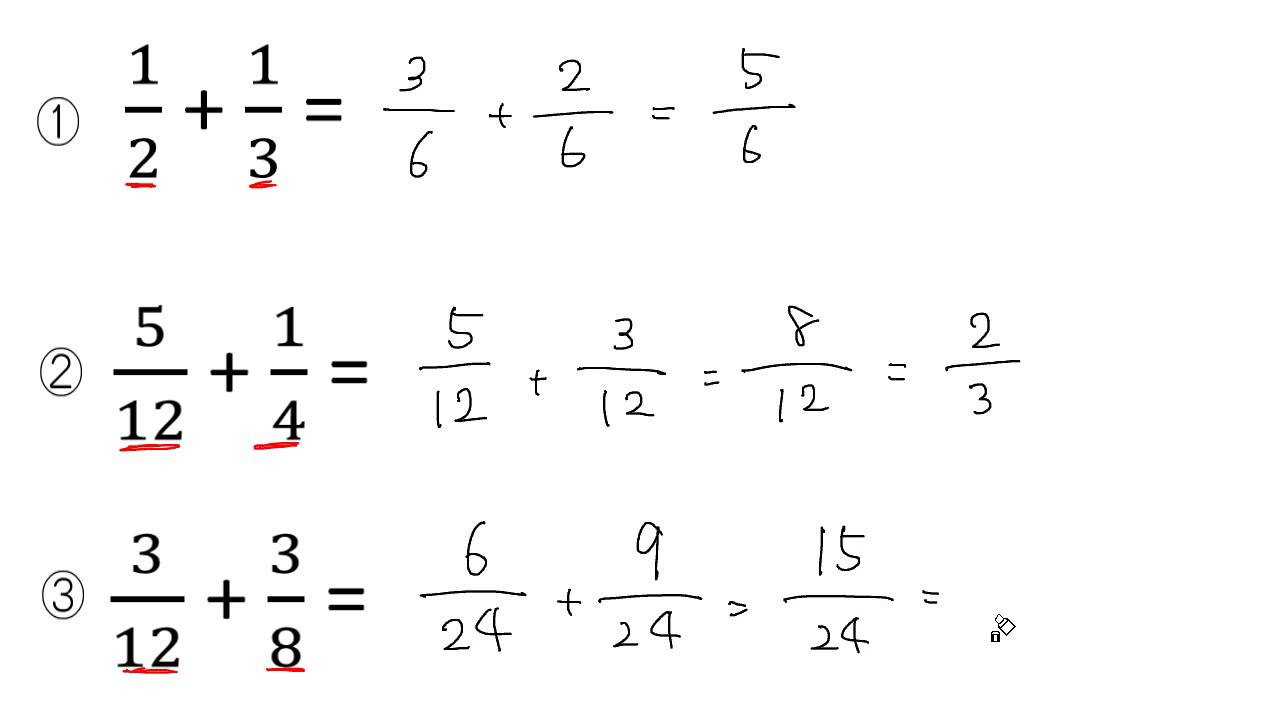
約分と通分 Ict教材eboard イーボード

等しい 分数 の やり方 分母がちがう分数を，大きさの等しい共通 な分母の分数に直すことを通分といいます。 ・既習事項をどのようにして考えたかを思い 出させ，自力解決の見通しがもてるよう分母がちがう分数を，大きさの等しい共通 な分母の分数に直すことを通分といいます。 ・既習事項をどのようにして考えたかを思い 出させ，自力解決の見通しがもてるようにす る。 ・それぞれのやり方を簡単に確認する。 手立て2「かく」活動 る。5 8 の 6 ント Pe う ME上 NGF FeCbエ。 。

５年算数分数 １ 通分約分の教え方

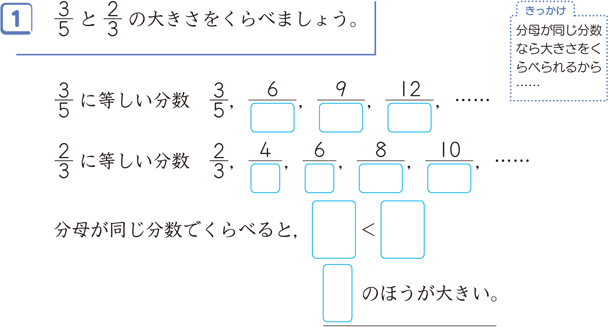
通分と約分 算数用語集

正負の数、分数計算のやり方を問題解説！ 正負の数の利用、平均を使った問題を解説！ 正負の数の問題まとめ！計算のやり方を確認しよう！ 文字式 文字の表し方を基礎から;帯分数→仮分数⑥ 帯分数→仮分数⑦ 帯分数→仮分数⑧ 帯分数→仮分数⑨ 帯分数→仮分数⑩ 帯分数→仮分数完成テスト 帯分数→仮分数進級テスト 分数 （等しい分数 基本編）トレーニング （無学年） 分数 （等しい分数 基本編）10回完成コース/学習管理表12 と6 の最大公約数は，6 と0 の最大公約数に等しい。 ゆえに，最大公約数は6 である。 このやり方をまとめる。 a;b の最大公約数は，割り算して， a ÷b = q r ゆえに， a = bq r ゆえに，a とb の公約数は，b とr の公約数に等しいから，最大公約数も同じになる

1

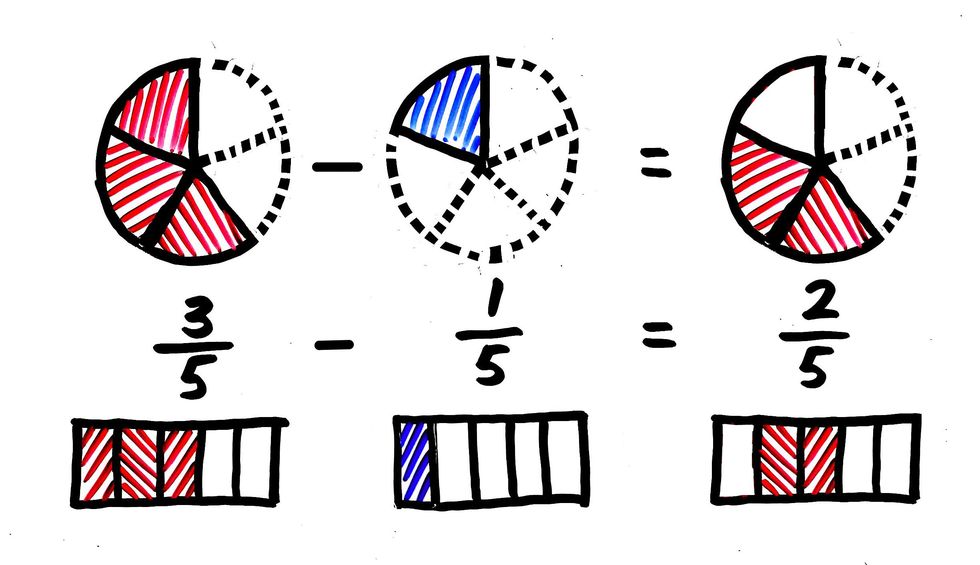
小学3年生で習う分数の足し算 引き算 計算のやり方と問題の解き方 そうちゃ式 分かりやすい図解算数 別館

 今回は分数の計算の1つ、分数の足し算のやり方と問題のとき方について書いていきたいと思います。 分数の足し算のやり方 ①分母をそろえる ②分子どうしを足す ③約分する 分母が同じ分数の足し算のやり方 分母が違う分数の足し算のやり方 分数の足し算に関する問題 問題① 問題②数学的な考え方 図や式を用いて，同分母の分数の加法の計算の仕方を考えている。 5 主な学習活動 指導計画における本時の位置づけ（全10時間） 第一次 1より大きい分数（3時間） 第二次 大きさの等しい分数（2時間）1 等しい分数 ・量分数の等しい分数 ・量でない数としての等しい分数 分数には分母や分子がちがう大きさ の等しい分数があることを理解する テープを使って30cm の 6 2, 3 1, 8 4, 4 2, 2 1 な どの分数の大きさを理解させる。 分数には分母、分子が違う大きさの等し

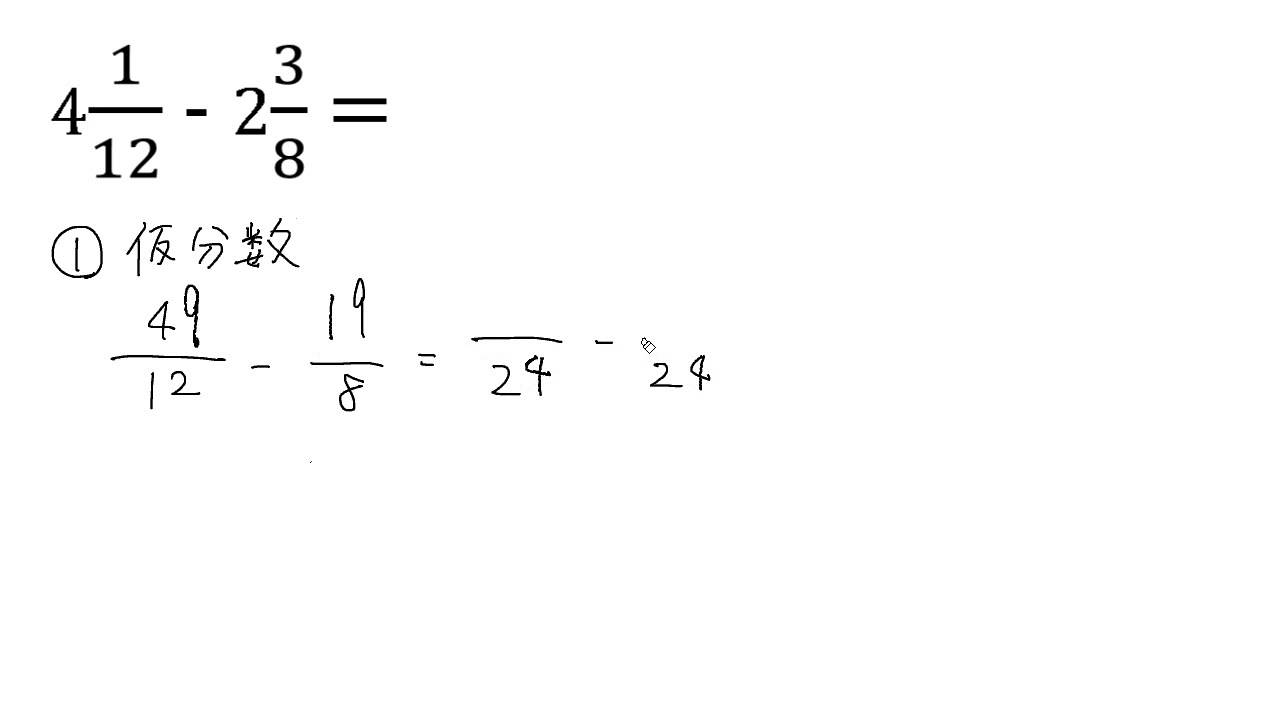
約分と通分 Ict教材eboard イーボード

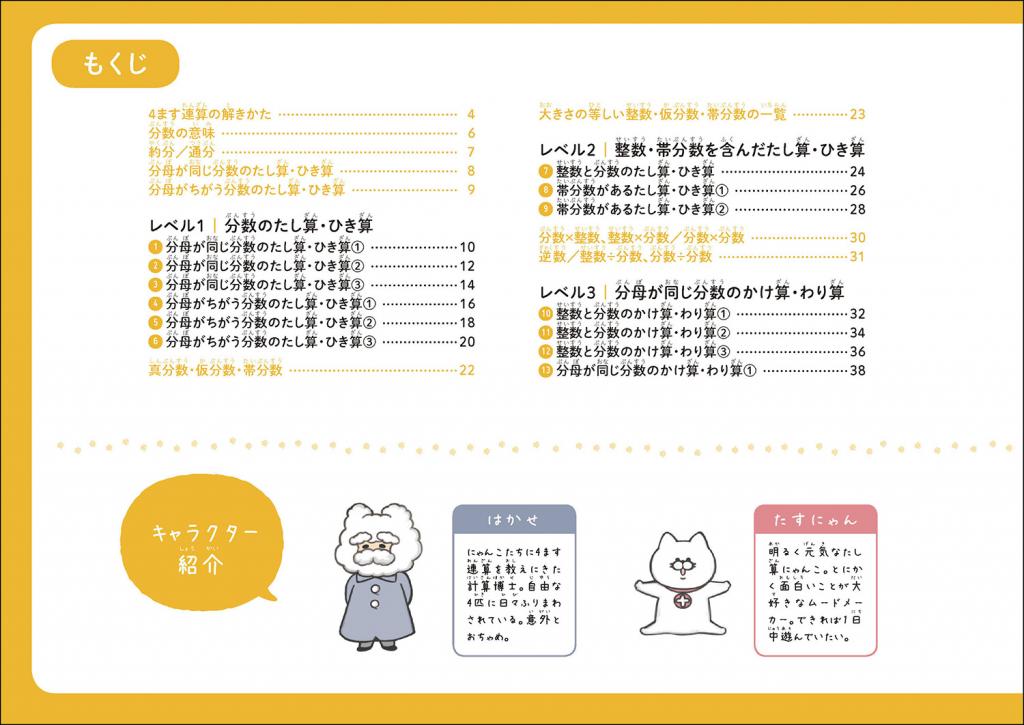
４ます連算 ４ます連算 分数編

等しい分数の見つけ方 「等しい分数」の見つけ方を学習する時間になりました。 まず前時にパターンブロックを使って見つけた「等しい」分数を並べ， 「これらを見て気がつくことはないかな。 と発問してみました。 この発問は本当はしたくない発問です。 前時に等しい分数を見つけ書き表した段階で，「あっ，おもしろいことがある。 」などの「呟き」と通分と最小公倍数 ≪解説≫ 通分と最小公倍数 幾つかの分数を分母の等しい分数に変形することを「 通分 」といいます。 分母の異なる分数の足し算や引き算を行うためには、先に通分しておく必要があります。 分数を正しく変形するには、分母と分子このような場合、小数は分数に揃えて逆算を進めるのが普通のやり方です。 逆算に良く登場する小数がありますので、これらの小数と分数が等しいことをしっかり覚えてください。 05 ＝ 1/2、025 ＝1/4、02 ＝ 1/5、0125 ＝1/8 等々 また、分数でも帯分数は仮

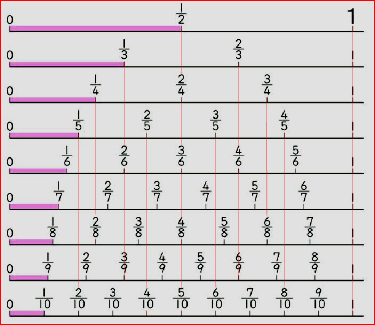
４年算数 分数 ２ わかる教え方のポンイト

小学５年生の算数 分数の約分 通分 練習問題プリント ちびむすドリル 小学生

です。 2つの分数を掛け合わせます。 16 1 × 8 5 = 128 5 {\displaystyle {\frac {16} {1}}\times {\frac {8} {5}}= {\frac {128} {5}}} 必要に応じて簡約化します。 128 5 = 25 3 5 {\displaystyle {\frac {128} {5}}=25 {\frac {3} {5}}}

大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ

小数を分数にするやり方 大人の学び直し算数 計算のやり方解説 無料

４ます連算 ４ます連算 分数編

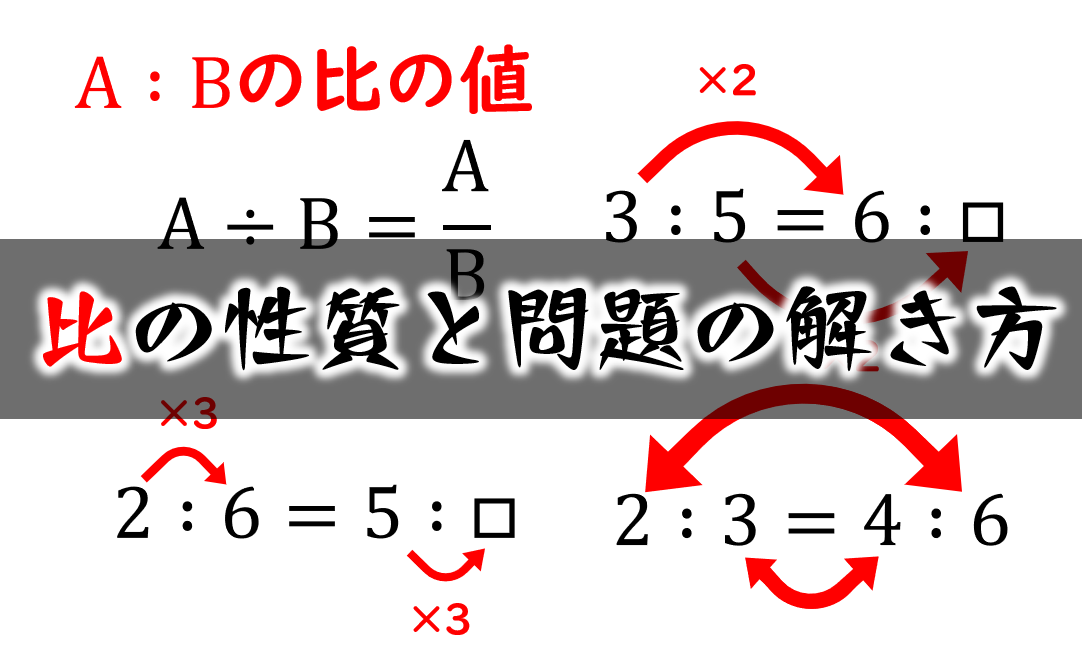
比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

６年算数比とその利用２等しい比の教え方

大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ

等しい分数 Youtube

分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun

分数 1 等しい分数 01 Youtube

整数に分数を足す計算のやり方は 1分でわかる計算方法 問題の解き方 引き算の方法

算数 小4 53 大きさの等しい分数 Youtube

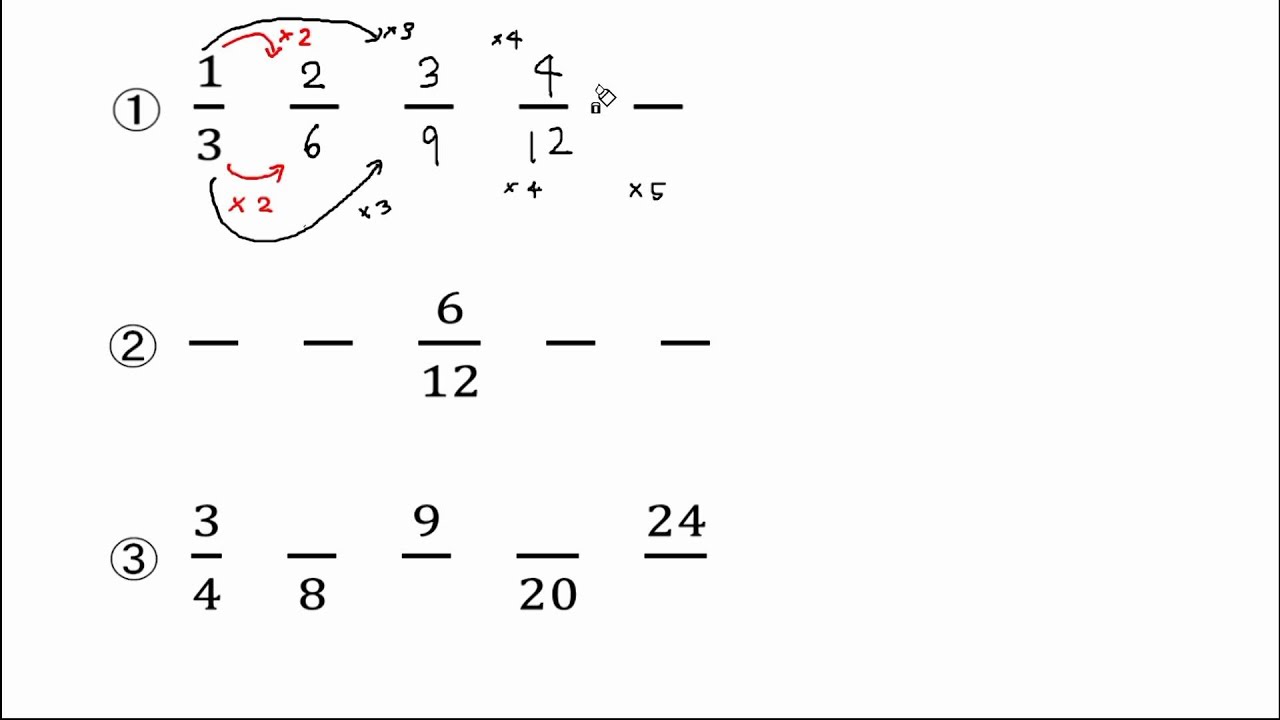
等しい分数をつくろう Youtube

小数を分数にするやり方 大人の学び直し算数 計算のやり方解説 無料

帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説

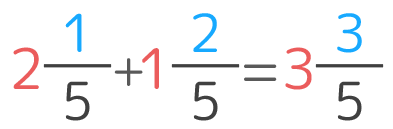
小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館

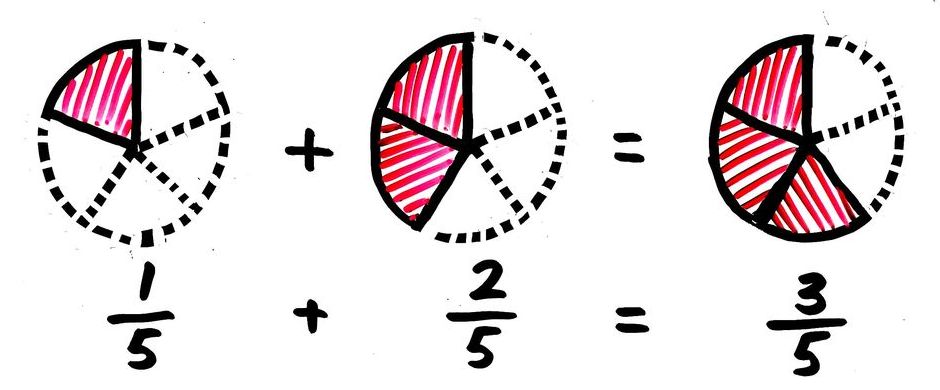
小学3年生で習う分数の足し算 引き算 計算のやり方と問題の解き方 そうちゃ式 分かりやすい図解算数 別館

算数小６の問題です 分数の比を簡単にするという問題です ６ Yahoo 知恵袋

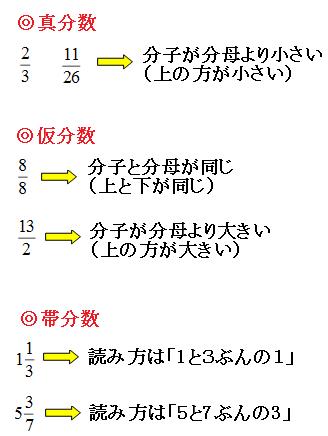
分数の基本をわかりやすく解説 分数とは何か を意識できれば超便利

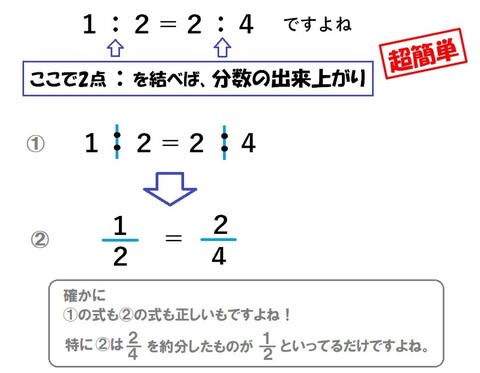
比と分数の関係 小６ 超重要で超簡単 比 分数の変形 算数の教え方教えますmother S Math Happy Study Support

一週間で完成 小学5年生への分数の教え方のコツ 約分 通分 足し算引き算 そうちゃ式 分かりやすい図解算数 別館

通分 Instagram Posts Photos And Videos Picuki Com

帯分数の足し算 のやり方帯分数について すっかりわすれてしまった高校生 Yahoo 知恵袋

等しい分数 Youtube

工夫して分数の計算 分数の教え方 学習 学習ノート 分数

５年算数分数 １ 分数たし算ひき算教え方

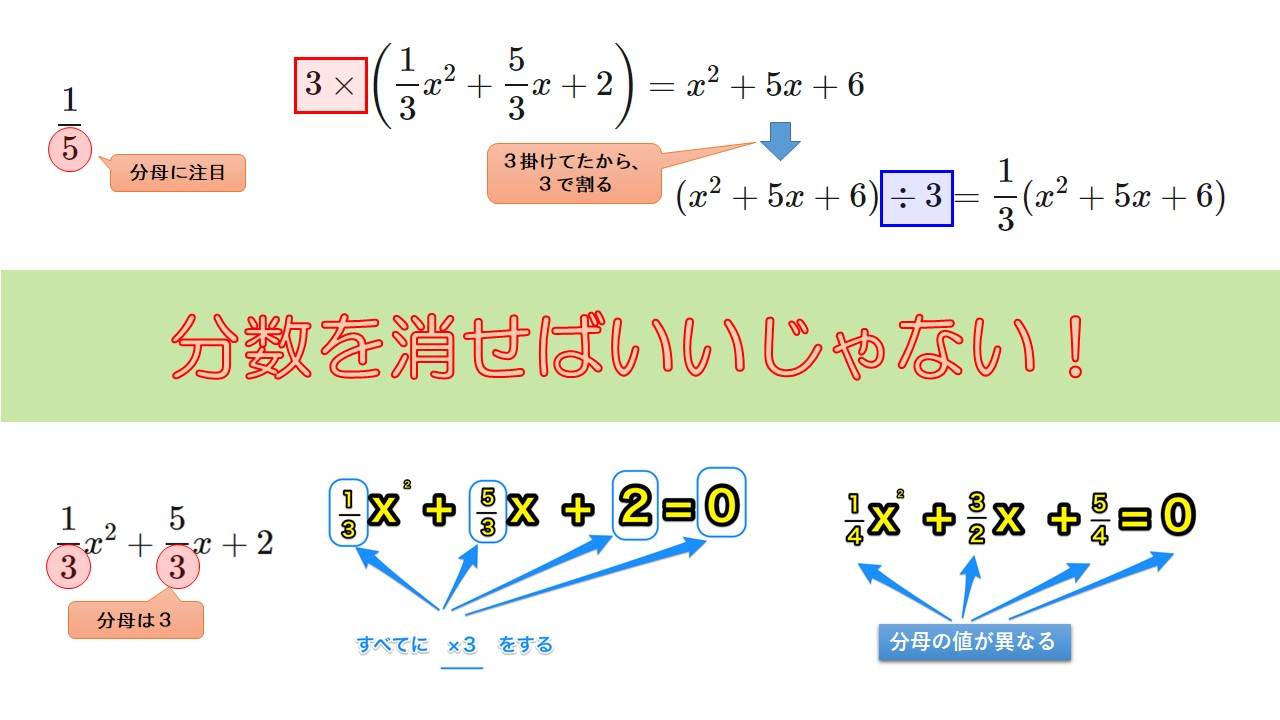
高校数学 因数分解 分数が登場する式を因数分解する方法 わかりやすく解説します 数学の面白いこと 役に立つことをまとめたサイト

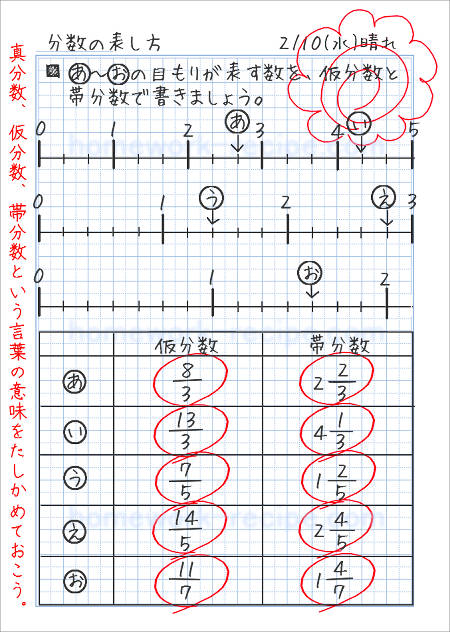
真分数 仮分数 帯分数の自主学習ノート 家庭学習レシピ

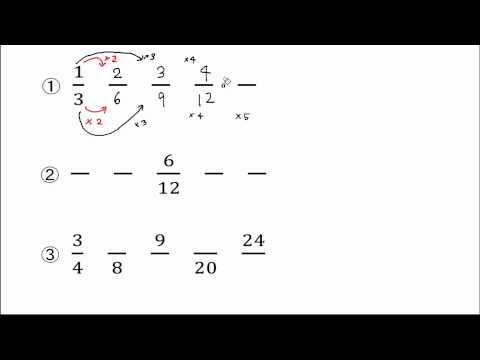
等しい分数をつくろう Youtube

通分と約分 算数用語集

４年算数 分数 ２ わかる教え方のポンイト

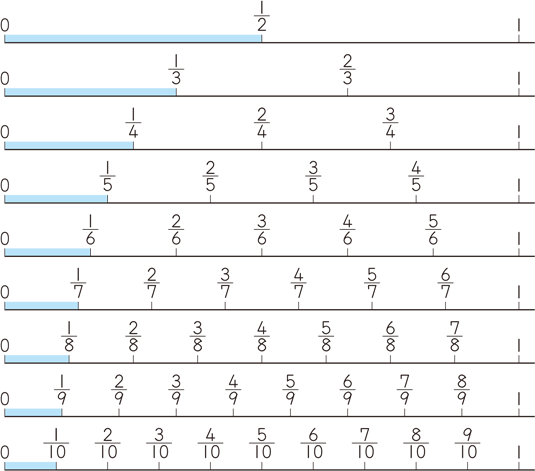
単位分数と分数の性質 算数用語集

帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説

4年 分数 等しい分数 Youtube

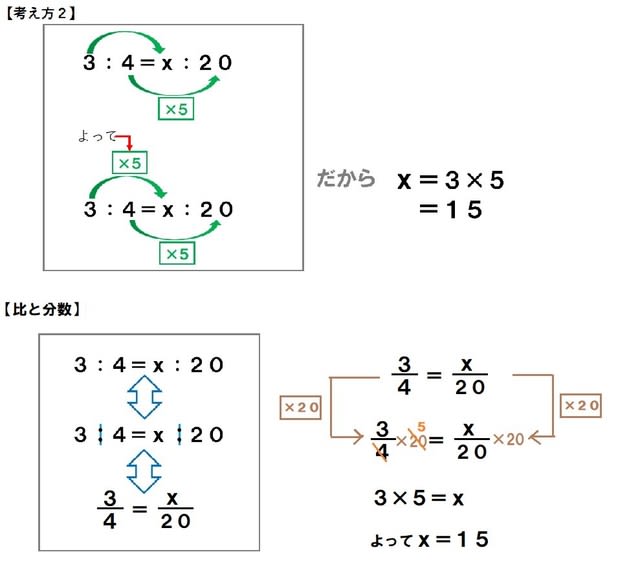
比の問題 小６ 比と分数の関係 算数の教え方教えますmother S Math Happy Study Support

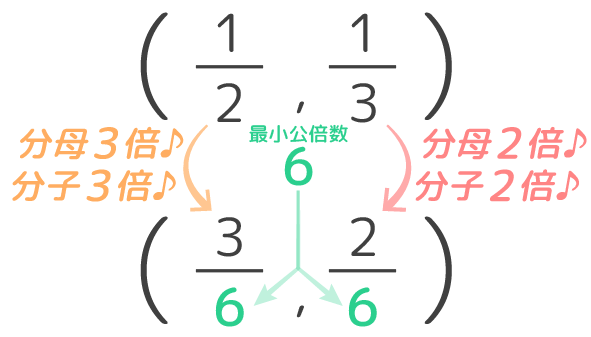
何年生で 分数の通分のやり方教え方と問題演習 3つの分数の通分も そうちゃ式 分かりやすい図解算数 別館

大きさの等しい分数は 線ですぐわかる 算数嫌い0 ゼロ 先生のブログ

小学校4年 5年 算数 同じ大きさの分数 Youtube

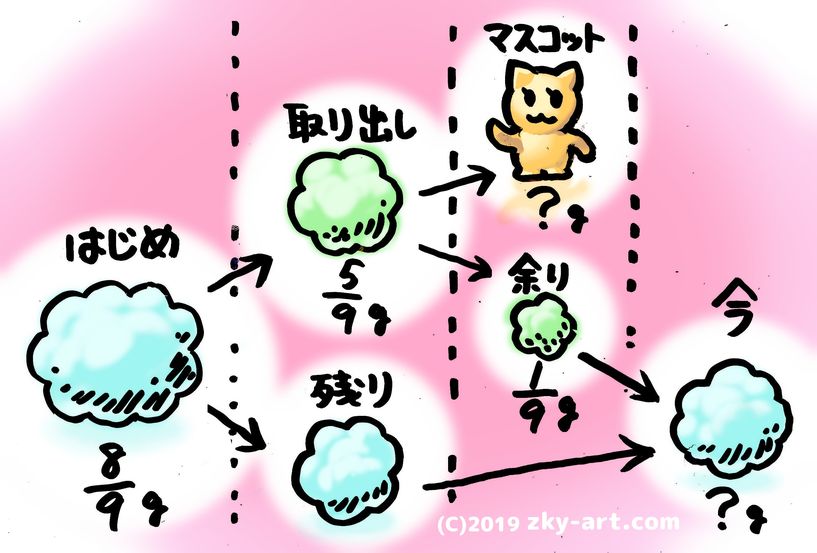
小学3年生で習う分数の足し算 引き算 計算のやり方と問題の解き方 そうちゃ式 分かりやすい図解算数 別館

４年算数 分数 ２ わかる教え方のポンイト

ポータルサイトトップへ 田村市教育ポータル

部分分数分解の公式 やり方と分数数列の和の求め方 理系ラボ

割合の表し方の１つとして 比について学びます 比とは 数の割合を A Bのように表したもの のことです A Bは 整数だけではなく 小数や分数であることもあります 例えば こ 学習ノート 学習 小学校 算数

Www Kyoiku Shuppan Co Jp Textbook Shou Sansu Files 2505 65 5 7 Kaito Pdf

４ます連算 ４ます連算 分数編

2分の1 2分の1の分数のやり方を教えてください 下のよう Yahoo 知恵袋

すきるまドリル 小学５年生 算数 分数のたし算とひき算 無料学習プリント すきるまドリル 無料学習プリント

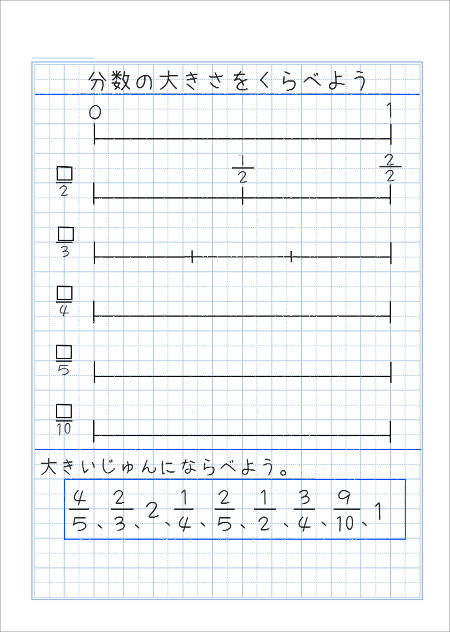
分数の大きさを比べよう 家庭学習レシピ

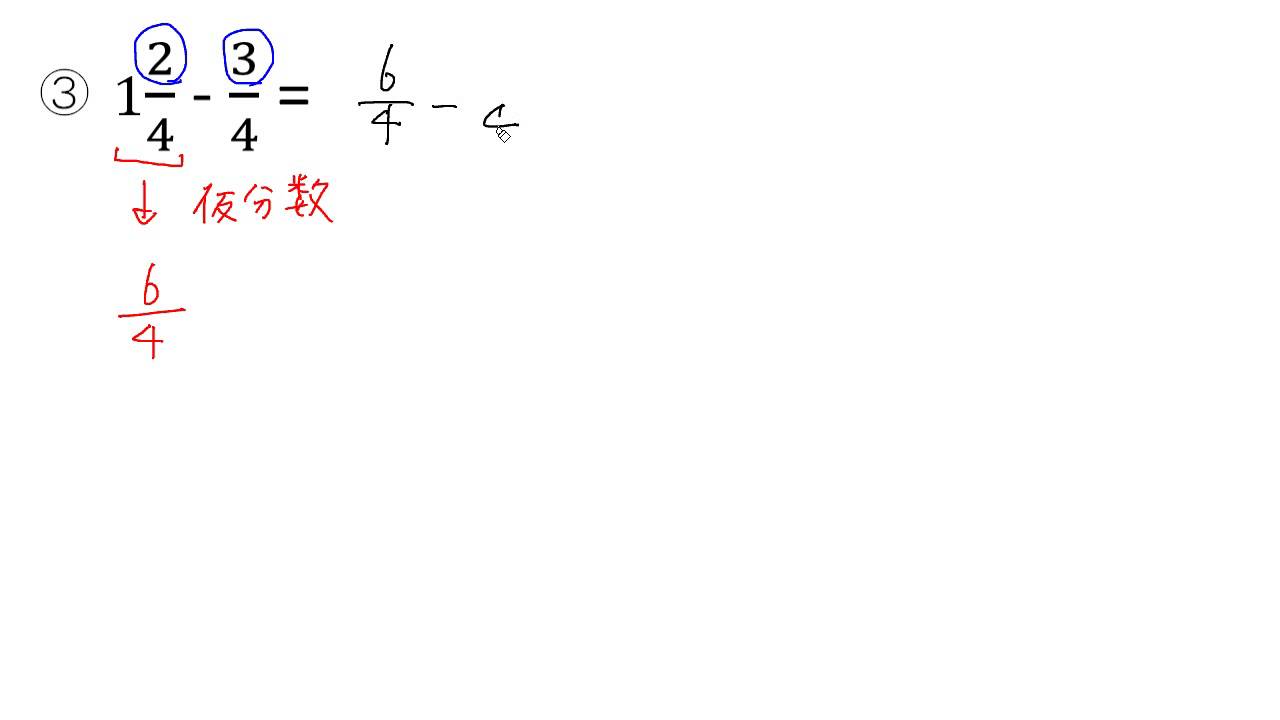
仮分数と帯分数 Ict教材eboard イーボード

Www City Saitama Jp 003 002 008 006 P D Fil San6 Pdf

3

比の性質と問題の解き方 小学生に教えるための分かりやすい解説 数学fun

Home Page V5 Cmovie 教育に特化した無料動画サイト シームービー オンライン学習サイト

６約分と通分２

無料でダウンロード 分数 の 大き さ ニスヌーピー 壁紙

Http Www City Kofu Yamanashi Jp Gakkoukyoiku Gakusui H21 Literacy Sansu Lt Sansu56nen1 Pdf

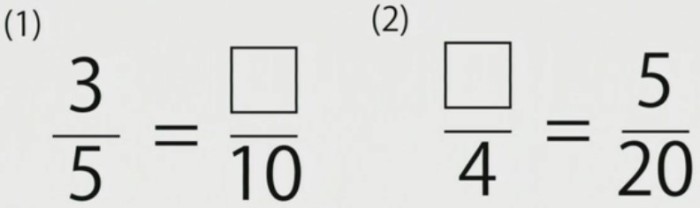
動画で学習 ２ 大きさの等しい分数 算数

分数 ひき 算

分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun

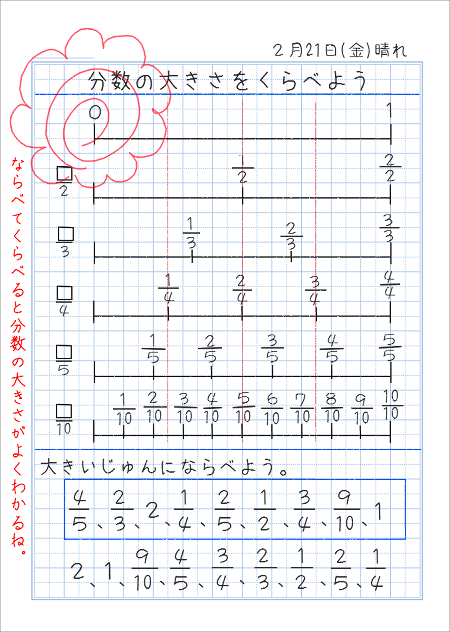
分数の大きさを比べよう 家庭学習レシピ

タッキー先生の おもしろ算数ゲーム 分数で遊ぼう コカネット

仮分数 帯分数 真分数とは 帯分数の掛け算などの応用問題４選も解説 遊ぶ数学

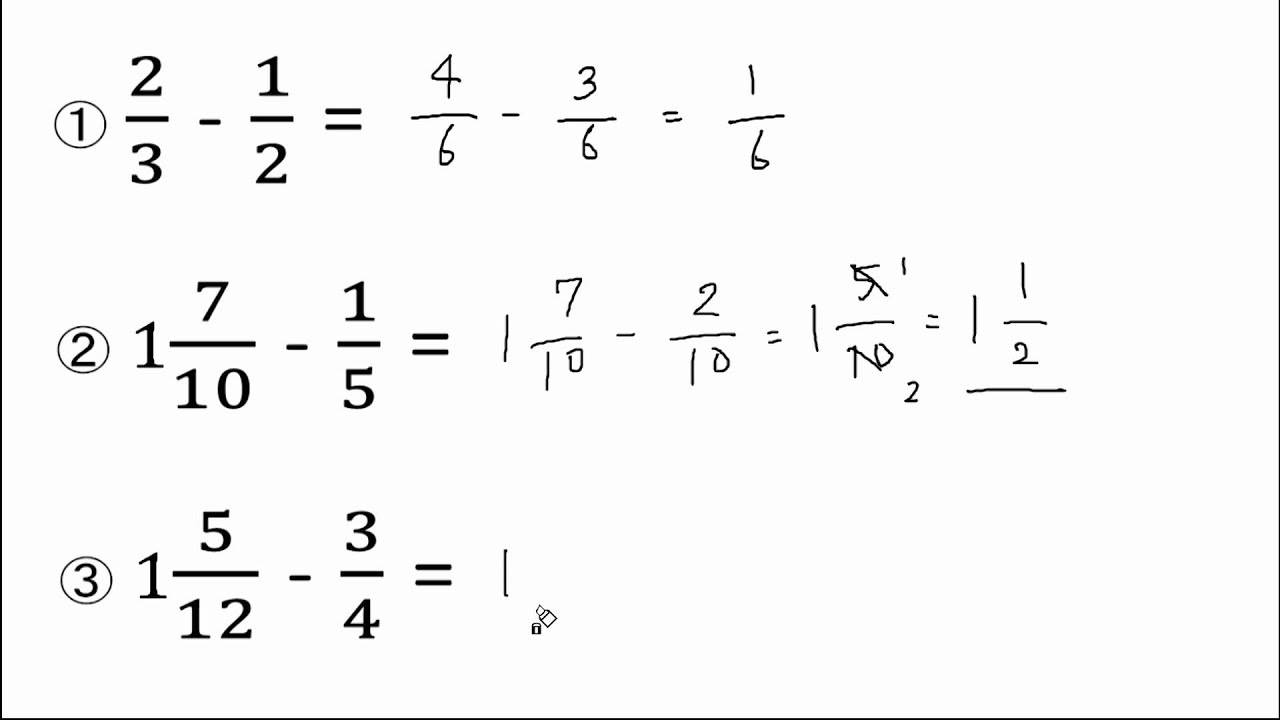
小学校5年 算数 分数のひき算 勉強 Youtube スタディチューブ

分数の大きさを比べよう 家庭学習レシピ

分数の足し算 引き算の計算方法 小学生に教えるための分かりやすい解説 数学fun

2

４年算数 分数 １ わかる教え方のポンイト

大きさの等しい分数を3つ書きましょうのやり方が分かりません教 Yahoo 知恵袋

Tossランド 向山型算数基本型ノート 小５ 分数

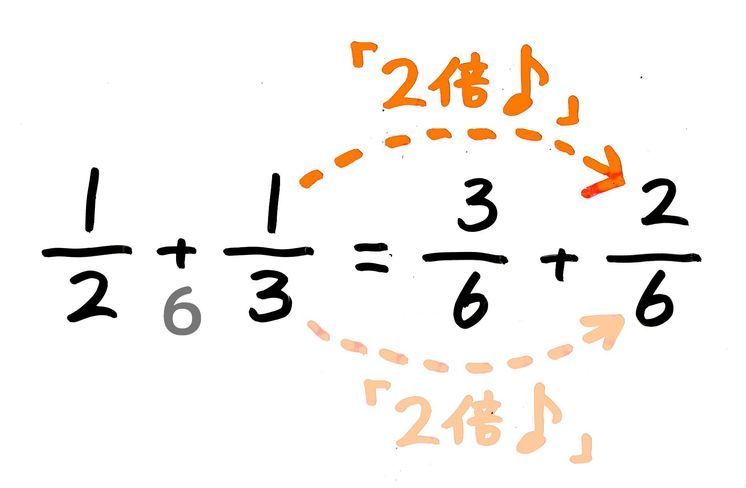
小5 異分母分数の足し算引き算の計算問題のやり方を図解 小6 中学受験生の復習にも そうちゃ式 分かりやすい図解算数 別館

仮分数 帯分数 真分数とは 帯分数の掛け算などの応用問題４選も解説 遊ぶ数学

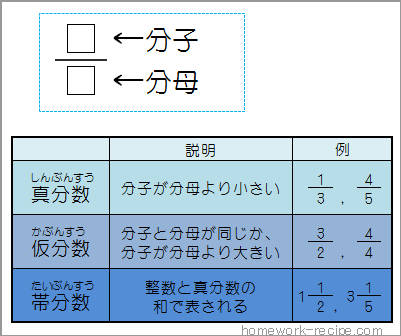
真分数 仮分数 帯分数の自主学習ノート 家庭学習レシピ

６約分と通分２

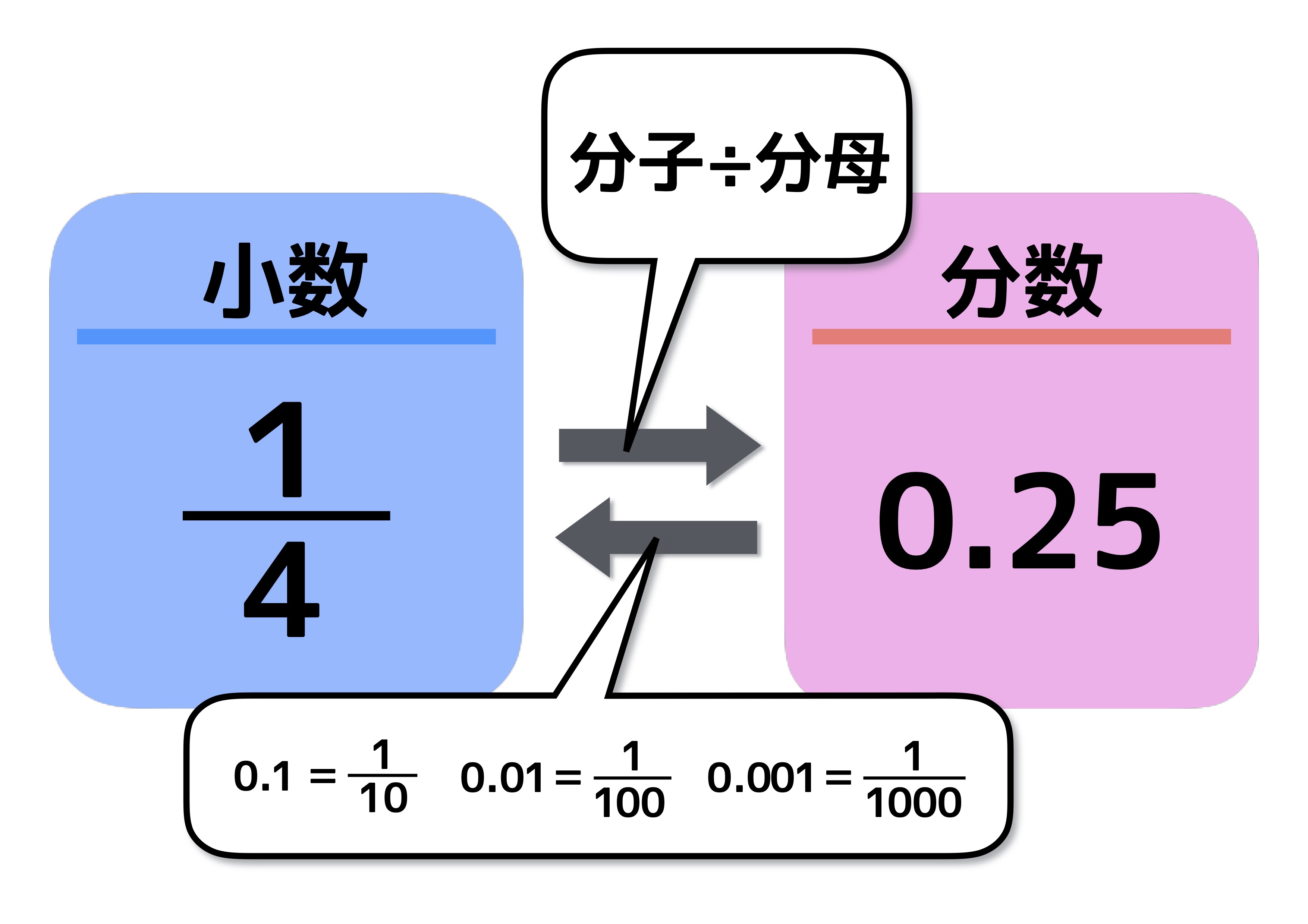
分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ

帯分数 仮分数 真分数とは 足し算や引き算など計算のやり方を わかりやすく解説

分数 1 等しい分数 02 約分 Youtube

5年生算数ドリル 分数 たし算 ひき算

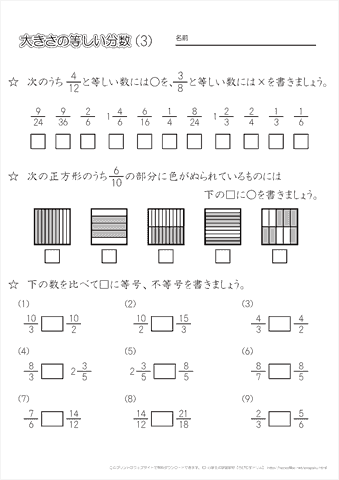
小学４年生の算数 大きさの等しい分数の理解 練習問題プリント ちびむすドリル 小学生

４年算数 分数 １ わかる教え方のポンイト

小4算数 スクールプレゼンター教材共有サイト スクプレ道場

Http Www Edu City Yokohama Lg Jp School Es Kawawahigashi Index Cfm 1 2430 C Html 2430 0430 Pdf

小学校5年生の算数 数学fun 数学 分数 算数

2

小5算数 大きさの等しい分数 Youtube

16 号 指導者用の参考書 Astamuse

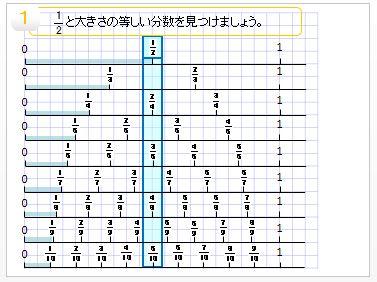
烏小ニュース H29 那須烏山市立烏山小学校

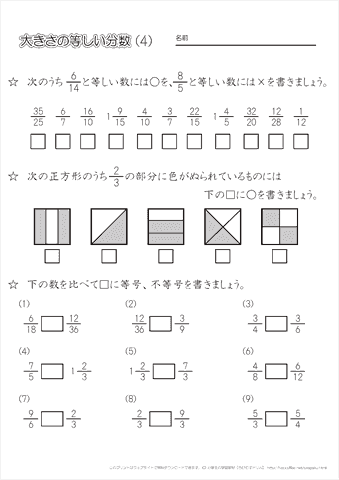
小学４年生の算数 大きさの等しい分数の理解 練習問題プリント ちびむすドリル 小学生

1

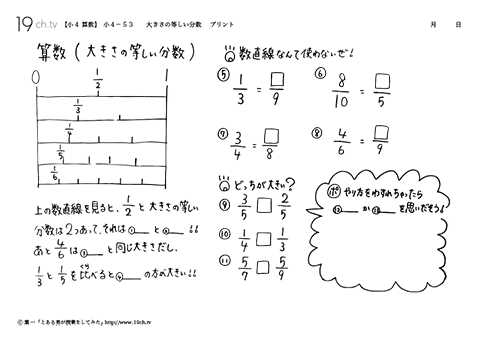
小学4年生の算数 動画 大きさの等しい分数の問題 19ch

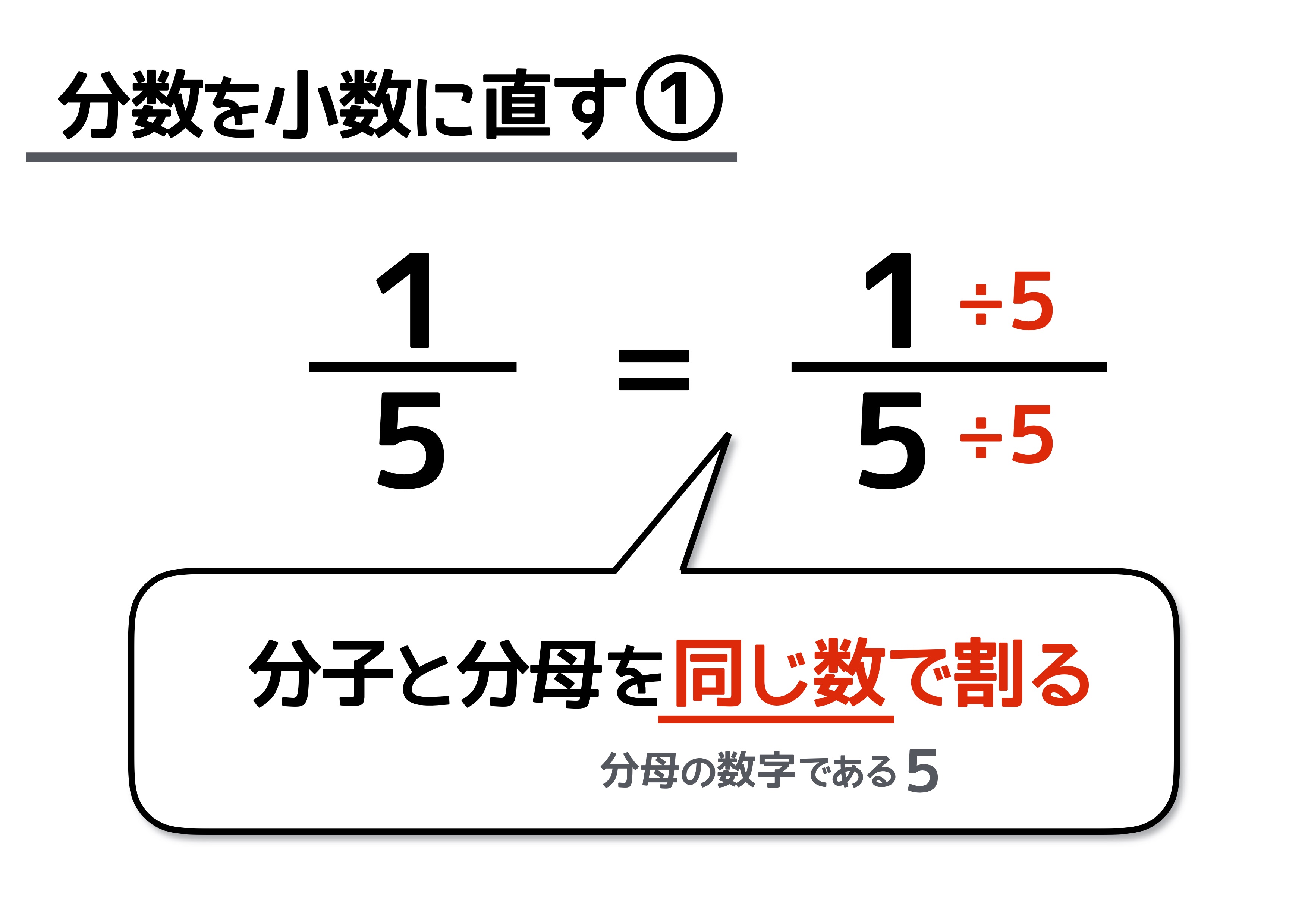
分数を小数に直すには 分数の計算でよく使う 基本知識 で簡単に理解しよう 中学受験ナビ

3