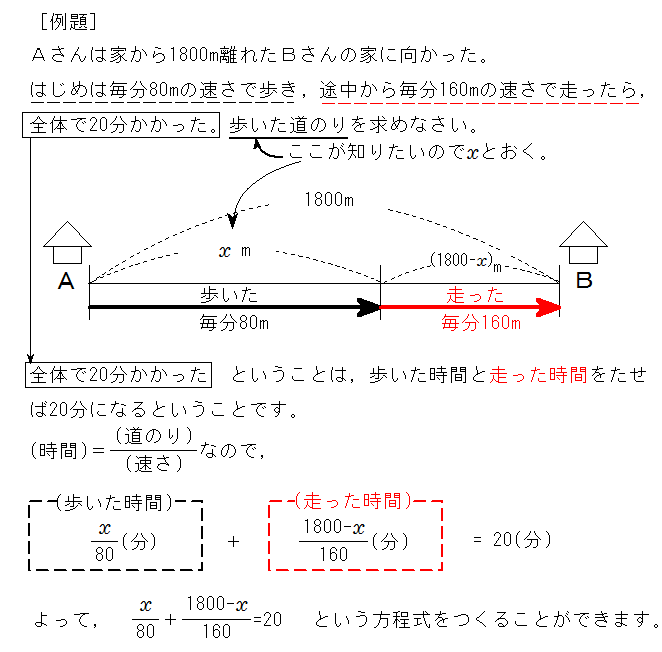
速さの問題 道のりで等式をつくる 追いかける 問題(2 学期中間) 兄がある地点を出発してから5 分後に,弟が同じ地点を出発して兄を追いかけた。兄は分 速80m,弟は分速180m で進むとするとき,次の各問いに答えよ。途中で速さが変わる問題に関しては,速さごとに区切って考えます。 そして,方程式をつくるときには,図で表すと文章をより わかりやすく理解できます。 例 Aさんは家から1800m離れたBさんの家に向かった。 はじめは毎分80mの速さで歩き , 途中から毎分160mの速さで走った ら, 全体で分かかった。 歩いた道のり を求めなさい。 ここが知りたいので x として難しいポイントを抑え、練習しましょう。 「速さ」は速度・時間・距離全ての要素を考慮しながら計算しないといけない ため、お子様が苦手とする範囲です。 しかし中学受験で頻出の旅人算にも影響します。 旅人算とは、逆向きに進む2人が途中で出会ったり、同じ向きに進む人に出会ったりする、速さの文章問題です。 同時に2人が動くので、お子様は混乱し
途中で速さが変わる速さの問題を解説 面積図を使って簡単解決
速さ 時間 距離 問題 中学
速さ 時間 距離 問題 中学-中学受験 4年 unit 411 速さ 速さと時間と道のり 例題と解説 トレーニング 確認テスト ログインが必要です 関連する過去問 5年生向け 吉祥女子中学校06 単位換算中学 数学一次関数 応用 速さの問題予習、復習、定期テスト対策としてご活用くださいチャンネル登録よろしくお願いします開明塾 大曽根




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
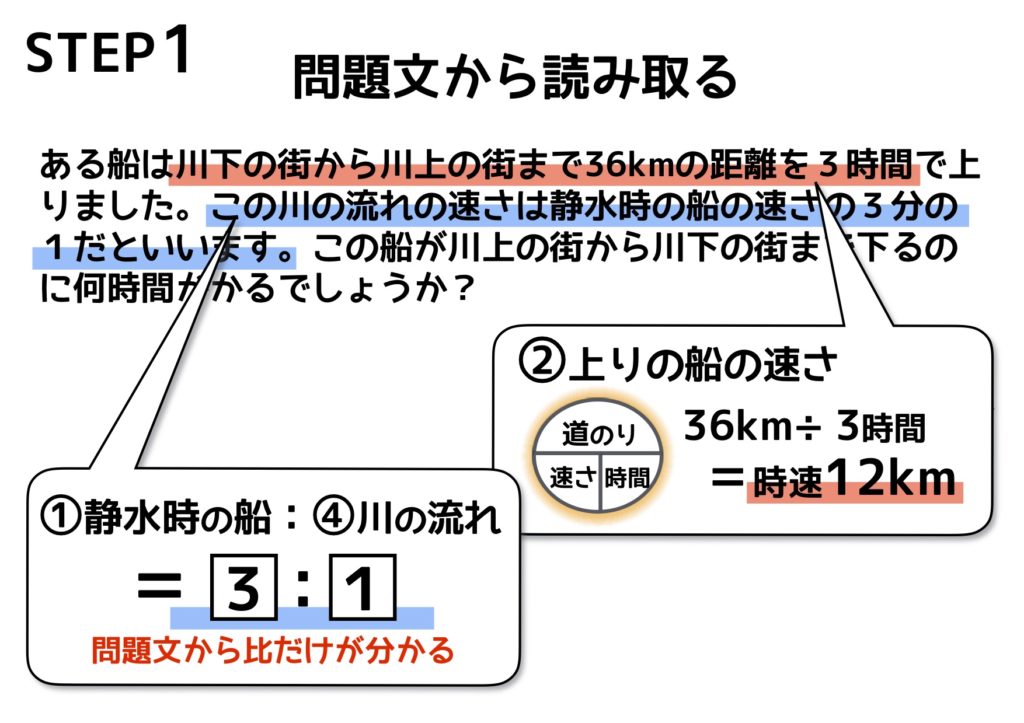
A地からB地を時速30km、B地からC地を時速40kmで進むと9時間かかる。 A地からB地を時速40km、B地からC地を時速50kmで進むと7時間かかる。 A地からB地、B地からC地の距離をそれぞれ求めなさい。 練習問題4 距離(道のり)=速さ×時間 速さ=道のり÷時間 時間=道のり÷速さ これは基本ですが、上記と同時に 1時間=60分 1分=60秒 1時間=3600秒 1分=1/60時間 1秒=1/60分 1秒=1/3600秒 この辺りをきちんとしておきましょう。 (最終的には)速さは、物体の速さを求めるには、時間と移動距離が必要になる。 ※速さの単位はメートル毎秒(m/s)や キロメートル毎時(km/h)などを使う。 速さm/s = 移動距離m 移動にかかった時間s 例題)ある物体が4秒間にm移動したとすると、この物体の
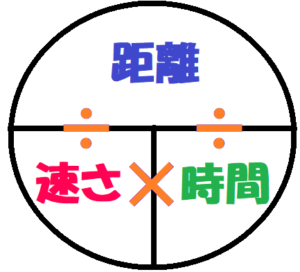
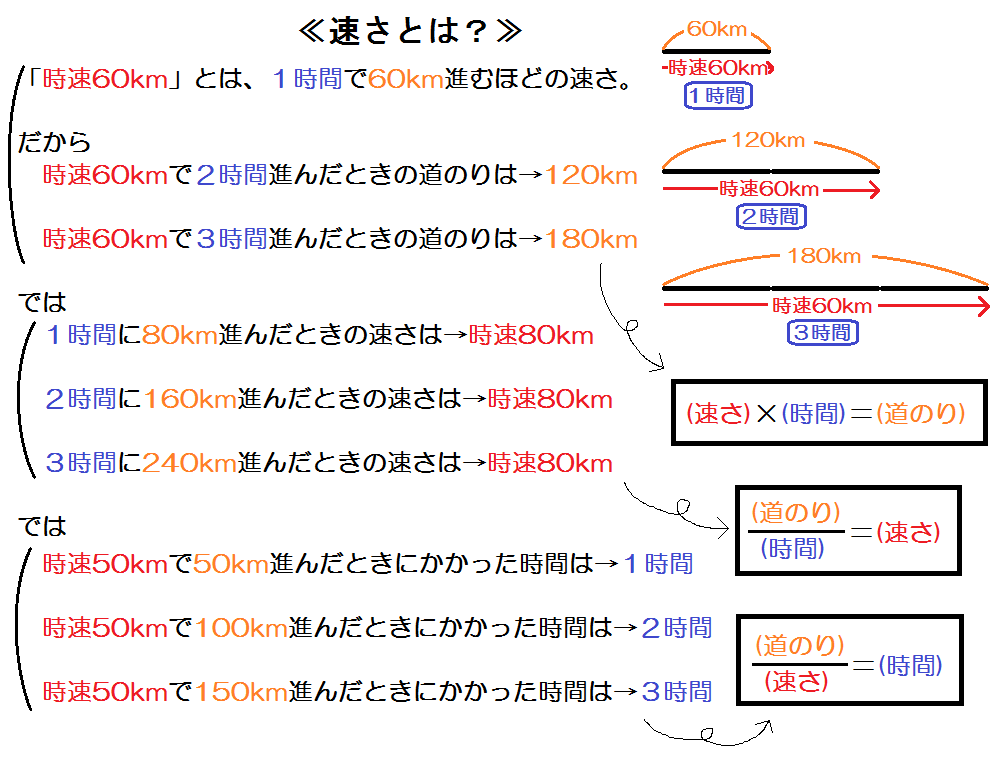
中学数学「一次方程式の利用」文章題「道のり・速さ・時間の問題」を丁寧解説 中学数学の基本「一次方程式」。 方程式の「利用」や「応用」というかたちで、文章問題が出題される単元でもあります。 別の記事でご紹介 した通り、文章問題は主に8例えば,自動車が3 時間で1km 走ったとき,1 時間あたり では,1(km)÷3(時間)=40(km)進んだことになる。このとき の速さは時速40km とも表されるが,ここでは,km/h(キロ メートル毎時)という単位を使って40km/h と表す。「h」は 「hour(時間)」の略である。時速50km(速さ)×2時間(時間)=100km(距離) つまり、 (速さ)×(時間)=(距離) だね。 あとはこの式を変形してやれば、 (時間)=(距離)/(速さ) (速さ)=(距離)/(時間) (距離)=(速さ)×(時間) 「速さ」「時間」「距離」の3つのうち、2つが分かっていれば、残りの1つは計算で求めることができる よ。
「距離×時間=速さ?!」 のような間違い方をしなくなります。 また、 「縦に速さ、横に時間」を書くくせ をつけておくと、 「速さのつるかめ算」のような中級問題にも 対応が可能です。 速さの単位換算では、 「時速 km÷36=秒速☆m」 というテクニックが、まず問題の前半部分「100mを走るのにAは16秒、Bは秒かかります。 」 ここで読み取りたいのは、 距離一定 です。 時間の比A:B=16:=4:5 速さの比A:B=5:4(時間の比の逆比です。 ) 次に後半部分「同時にスタートして100m走ったとき、Aがゴール速さ×時間=距離 を使おう 「速さ=時速4km」「時間=x時間」のとき、「距離」を求める問題だね。 文字xが出てきたときも、ハジキの法則を使って考えよう。 速さ×時間=距離 4×x= 4x(時間) が答えだよ。 ①の答え




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
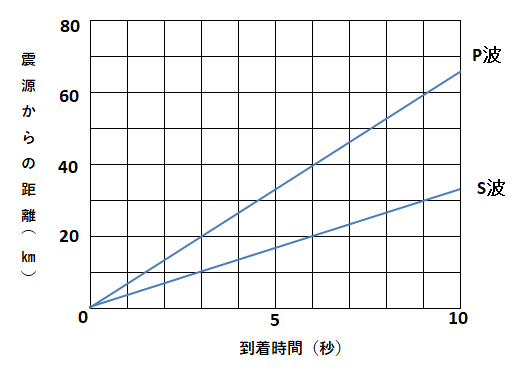



中1理科 地震の波の速さの計算練習問題 中学生勉強サイトあかね先生
歩く速さが変わる問題(中学受験算数 速さ) 通過算+旅人算(中学受験算数 速さ) ややこしい速さの問題(中学受験算数 速さ) 誰がいちばん速い?(慶應義塾中等部 10年) 時間が同じ場合の速さと距離(智弁学園和歌山中学 10年)速さ(スピード)が違うものが出てくる のが速さの鶴亀算です。 歩きと自転車というパターンの問題もあります。 合計の距離と時間が決められていて、それぞれの時間を求めるというのが典型的な問題です。 解き方は普通の鶴亀算と同じです。この問題は(1)→(2)→(3)のように「誘導形式」となってますので、 速さを学んだばかりの5年生にはちょうど良い復習問題 とも言えそうです。 (1)は、「距離÷速さ=時間」で計算できます。 1km÷時速4km-1km÷時速6km=1/12時間→5分 (2)は「親切」ですね。 通常ですと、




中学数学1年 1次方程式の利用 速さ 時間 道のり 受験の月




中1数学 方程式 23 2 中学数学高校数学個別指導in山形市 数専ゼミ
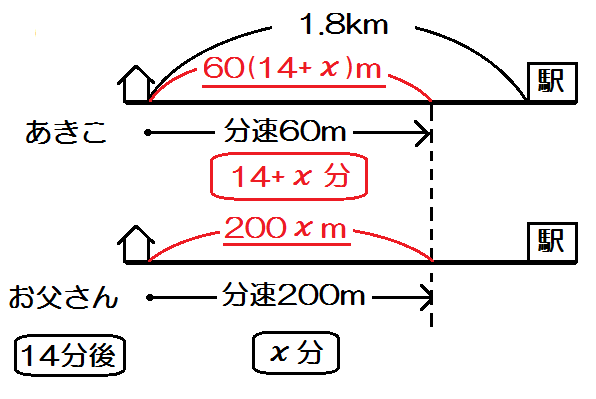
速さの単位とは? 冒頭で定義を示したとおり、速さとは「単位時間あたりに物体が移動する距離」のことです。 つまり、 時間;文章題(速さ) 「追いつく1」 注意点 表にまとめる 求めるものをxにする。 先に出た人と後から出た人の 距離は同じ 。 歩いていた(走っていた)時間は 先に出た人のほうが長い 。 例題 弟が家を出て毎分80mで歩いて行った。兄がその5分後に毎分100mで追いかけた。中学1年生の数学の練習問題 (距離と速さと時間の関係で1次方程式の文章問題) 標準レベルの問題です。 家庭学習の時は、問題文もノートに書くようにしましょう。 (問題文のパターンを書いて覚えることが大事です。




等速直線運動公式 グラフの書き方が中学生でもわかる記事 高校生向け受験応援メディア 受験のミカタ
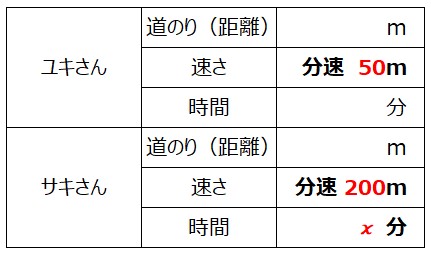



わかる 中学数学 一次方程式の利用 文章題 道のり 速さ 時間の問題 を丁寧解説
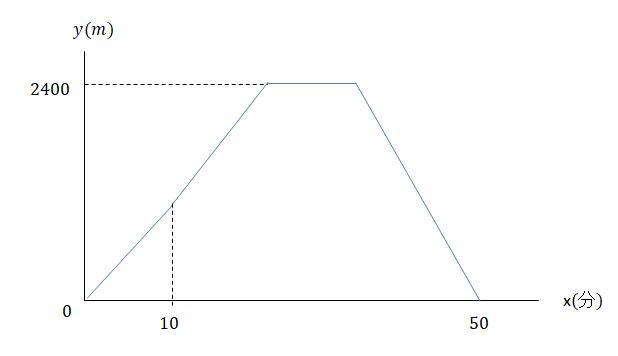
(1) 縦軸に速さ、横軸に時間のグラフでは、距離はグラフの何になるか。 (2) 縦軸に距離、横軸に時間のグラフでは、速さはグラフの何になるか。 (3) 等速直線運動について 縦軸に距離、横軸に時間をとるとどんなグラフになるか下のア〜エから選べ。 求める時間をxとおいたので、左辺も右辺も、同じもの、距離で表わして、等号で結びます。 最後に、この問題だと、反対方向に進む問題なので、 1人の進んだ距離+もう一人の進んだ距離=池1周の長さ が使えます。 距離=速さ×時間ですから、 65x55x=480道のり=速さ×時間 でしたね。 というわけで 弟の道のりを求めていくと 速さが50、時間が(x +8)なので 道のりは50(x +8)と表せます。 兄の道のりも同様に 速さが70、時間が x なので 道のりは70 x と表せます。 それぞれの道のりが求まれば 最後の仕上げ!




速さと時間から道のりを求める問題 家庭学習レシピ



1次方程式 速さ 中学から数学だいすき
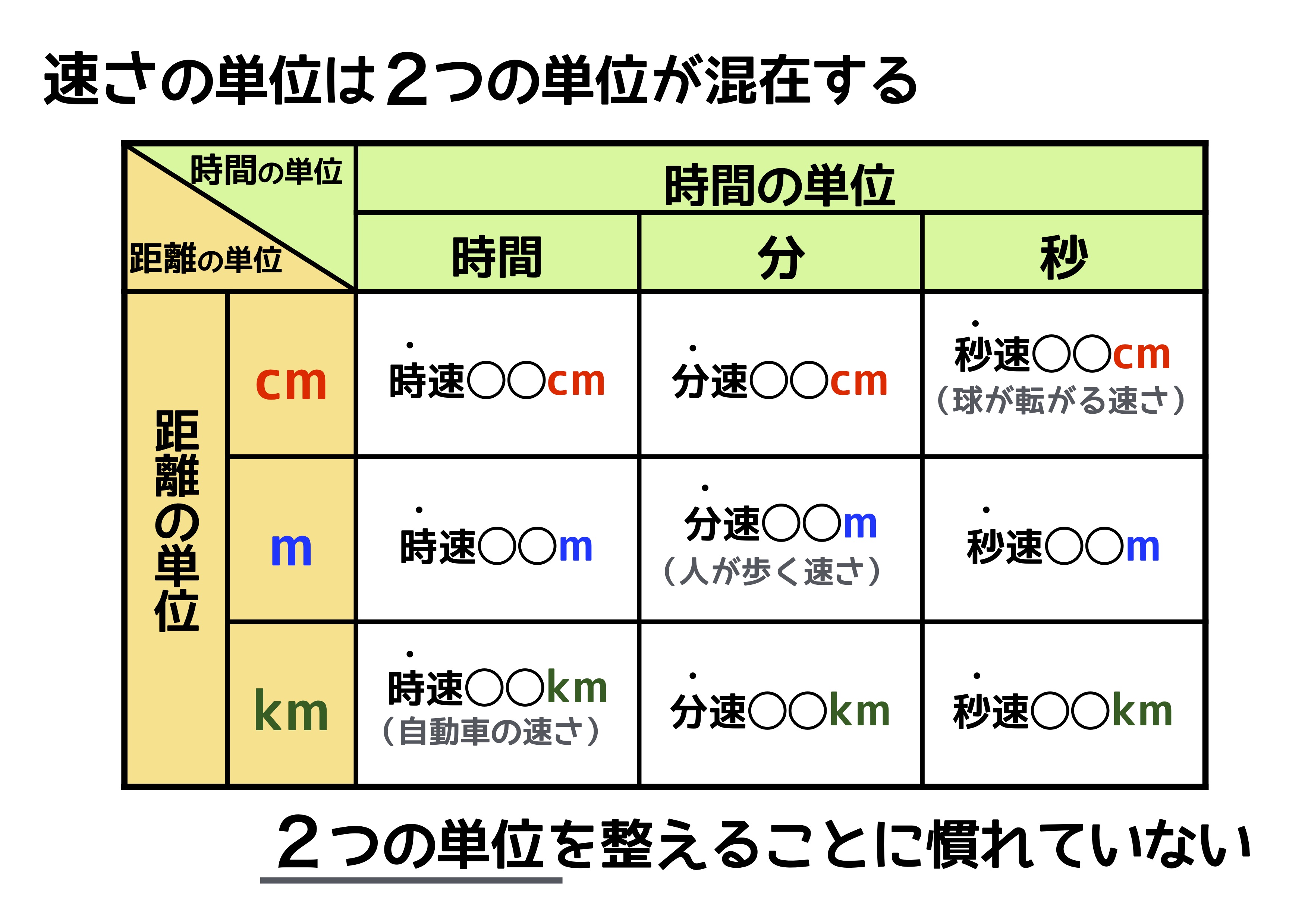
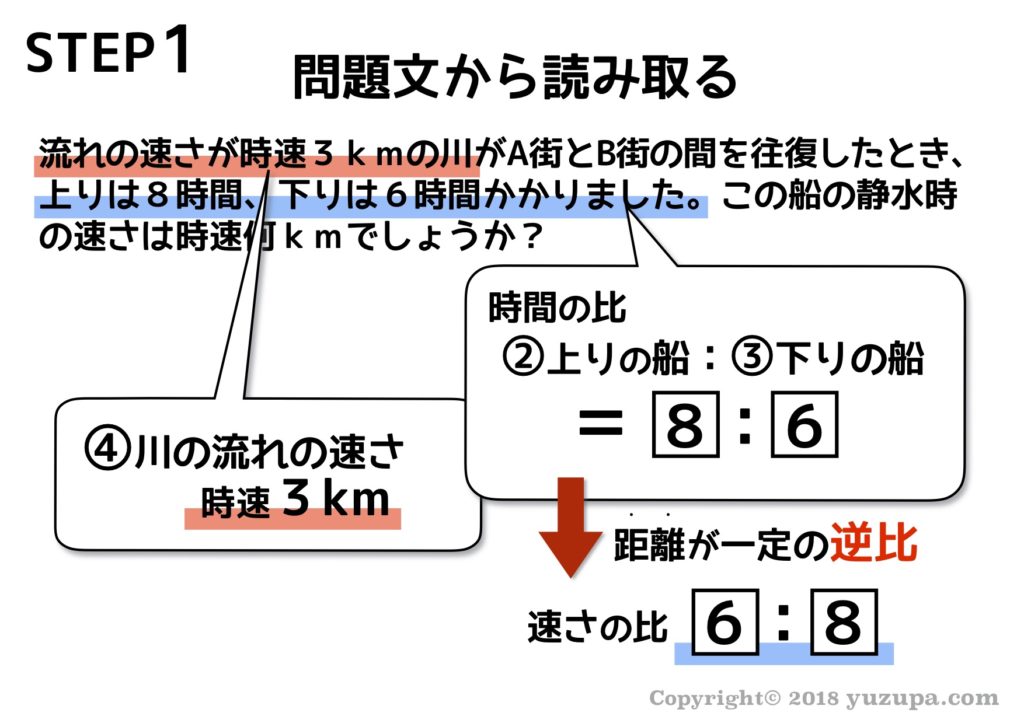
時間を求める問題ですから,速さと距離がわかれば答を出せます。 答 案 ・速さを問題で与えられていて,90㎞/時です。 =m/時 ① ・さて,列車が動く距離ですが, ⇒ここが鉄橋の問題を解くときの鍵になる部分です。 小学校算数の 速さの問題(旅人算)では、「同じ時間に進む距離 と 同じ距離を進む時間は 逆比である。」事を使うと、解答時間が短くなる問題もあります。そういった問題を実際に解いてみましょう♪|中学受験を体験したパパが解説する算数教室。という、 $2$ つの単位が組み合わさってできている $1$ つの単位である 、といえます! これが、「速さってややこしい」と感じる大きな原因の一つで



つるかめ算 速さの問題 の解き方を解説




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく
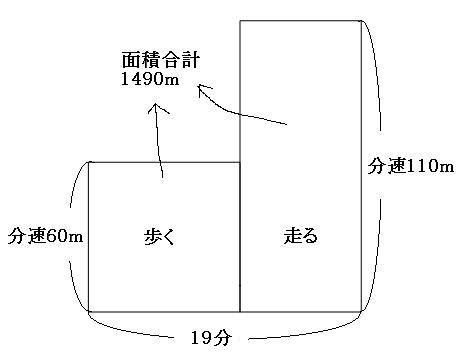
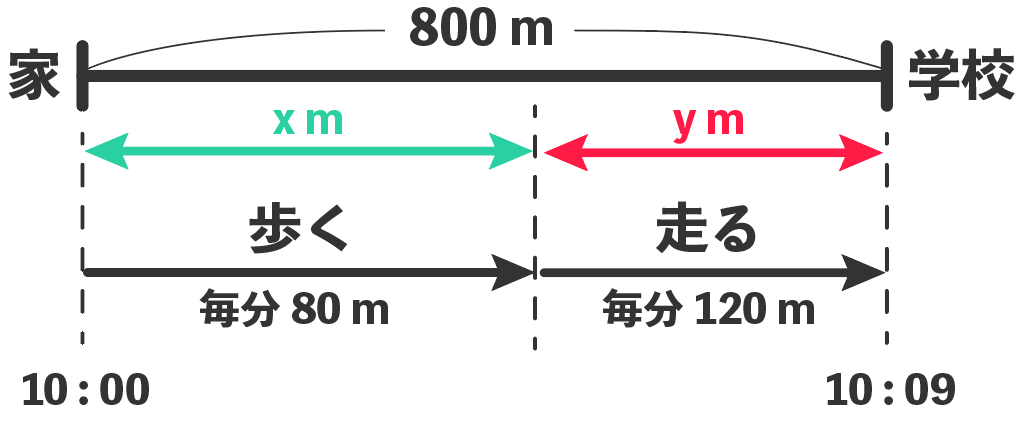
50x40 (17x)=800 答12分後 (3)式A君が歩いた時間をx分とする。 60x=100 (x6) 答10時15分 (4)式A町からB町までの道のりをxkmとする。 x 5 22x 4 =5 答10km (5)式A町からB町までをxmとする。 x 80 x 50 =52 答1600m 中学校英語学習サイト 中学英語の文法、練習問題、リスニング 中学校数学学習サイト 中学数学各単元の要点と練習問題2 人が出会うまでにかかる時間 (分)を x とする。 STEP2:等しい数量の関係をみつけ、方程式をつくる Aの歩いた距離 Bの走った距離 = 池の周りの距離 より、 80 x 170 x = 3000 STEP3:方程式の解を求める 80 x 170 x = 3000 x = 12 STEP4:問題に適しているか解答 (1)兄が家を出発してから弟に追いつくまでの時間を x 分とする。 2人の進んだ距離を数式で表し、等式を立てる。 弟 兄 速さ 60(m/分) 210(m/分) 時間



中学数学 攻略 速さの文章問題 数樂管理人のブログ




中1数学 方程式 22 1 中学数学高校数学個別指導in山形市 数専ゼミ
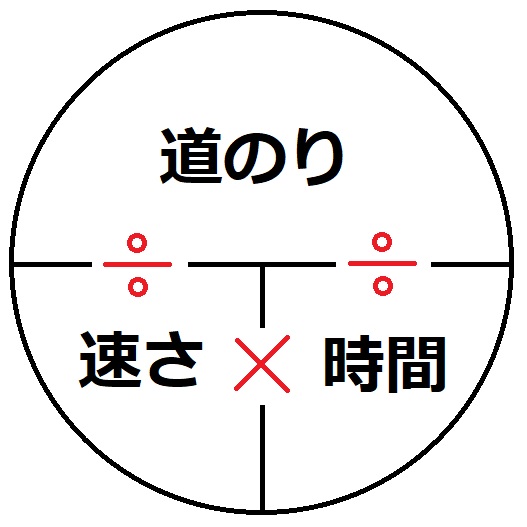
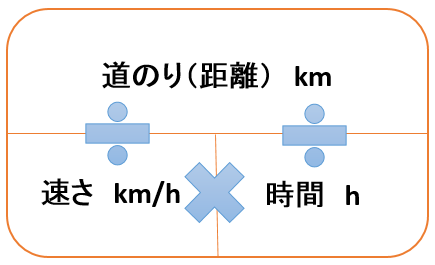
公式 速さ= 道のり 時間 、 道のり=速さ×時間、 時間= 道のり 速さ 例 400mの道のりを歩くのに5分かかった。 速さ = 400÷5 = 80 (m/分) 10mの道のりを、50m/分の速さで歩いた。 かかった時間 = 10 ÷ 50 = 24 (分) 30km/時の速さで4時間走った。 進んだ道のり = 30 × 4 = 1 (km) x (km)の道のりを、60 km/時で進んだ。X の方程式を解くと 100x=80x480 x=480 x=24 問題12 家から学校まで歩くときに,毎分 80 mの速さで歩くときと,毎分 100 mの速さで歩くときを比べると,毎分 80 mの速さで歩く方が 6 分多くかかった. (1) 毎分 100 m歩くときにかかる時間を x 分とおいて,毎分 100 mで歩いたときの距離を左辺とし,毎分 80 mで歩いたときの距離を右辺として,それらが等しいことを x の方程式の速さは時速 kmになります。 (8) 行きに時速4kmの速さで45分かけて進んだきょりを帰りは時速24kmの速さで 進みました。平均の速さは時速 kmです。 (9) 24kmのきょりを行きは時速8kmで、帰りは時速 kmの速さで進んだところ、平均 の速さが時速6kmになりました。




灘中算数17二日目2番 2 速さについて 算数ソムリエブログ 中学受験突破のために




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい
速さの三公式「みはじ」を覚えただけでは、速さ、旅人算、流水算の問題は手ごわい。 苦手だな、混乱するなというときには、速さの本質的なコンセプトをあらためて見直してみましょう。 道のり(距離)=速さ×時間 速さ=道のり (距離)÷時間 時間=道のり(距離)÷速さ速さが「時速」と書いてあるのに、 時間が「分」で与えられたので、 単位がずれて困ったのですね。 大丈夫、すぐに解決できますよ! ★ 単位のそろえ方 を以下で解説するので、 しっかり読んでくださいね。 中学生に多い、「速さの変換」のお悩み学校に行く旅人算(高輪中学 14年) 速さの比、時間の比は?(明治大学付属明治中学 12年) 通過算?旅人算?(15年 横浜共立学園中学) 速さと時間と距離(15年 雙葉中学) 明子さんは分速何mで歩いた?(浦和明の星女子中学 12年)
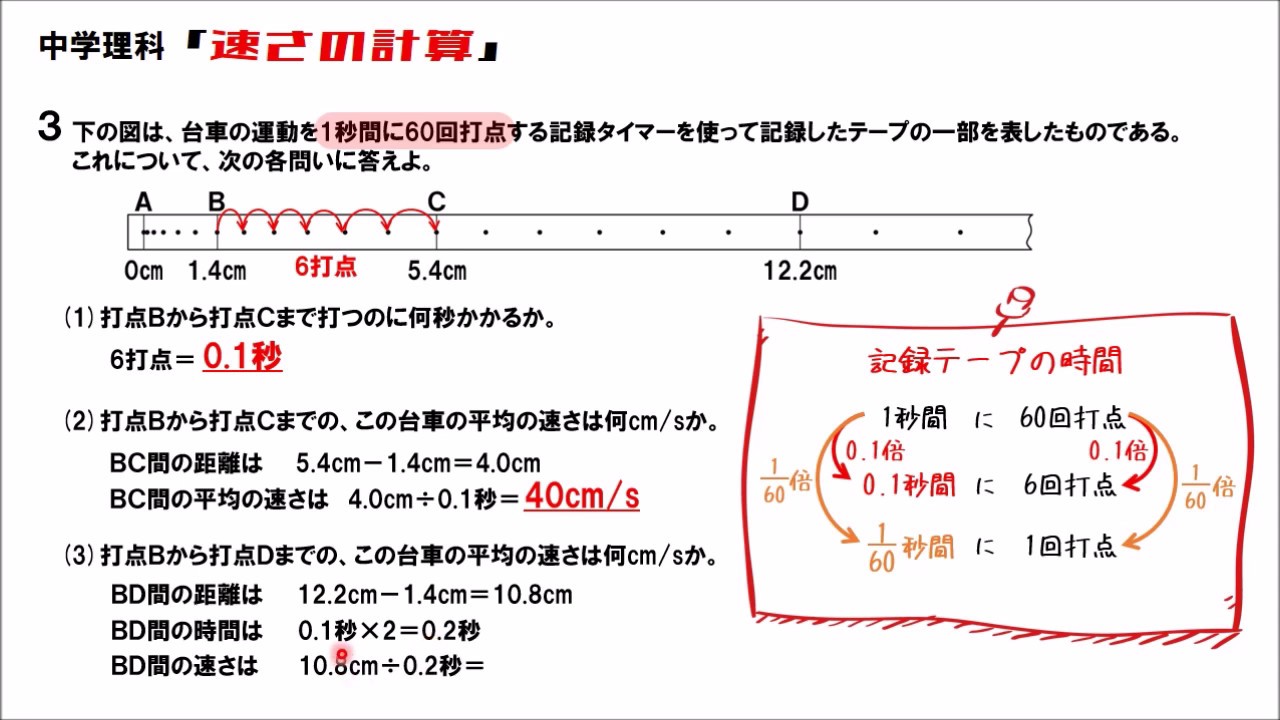



中学理科 速さの計算 Youtube



速さの計算 3 0 0 あらためてコンセプトなどを By Samekard Works Medium
速さ、時間、距離 車の走った距離は? (第6回ジュニア算数オリンピック、ファイナル問題より) 道のりは何km? (第3回算数オリンピック、決勝問題から) 池の周囲の長さは何mですか? (第12回算数オリンピック、トライアル問題より) 何分かかる
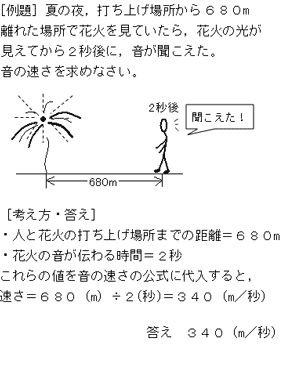



光 音 力 圧力 音の速さの求め方がわからない 中学生からの質問 理科 進研ゼミ中学講座 中ゼミ




理科の平均の速さはどうやって求めますか Clear




中学受験 算数 速さの重点ポイントまとめ 比を使った裏技公開 中学受験アンサー



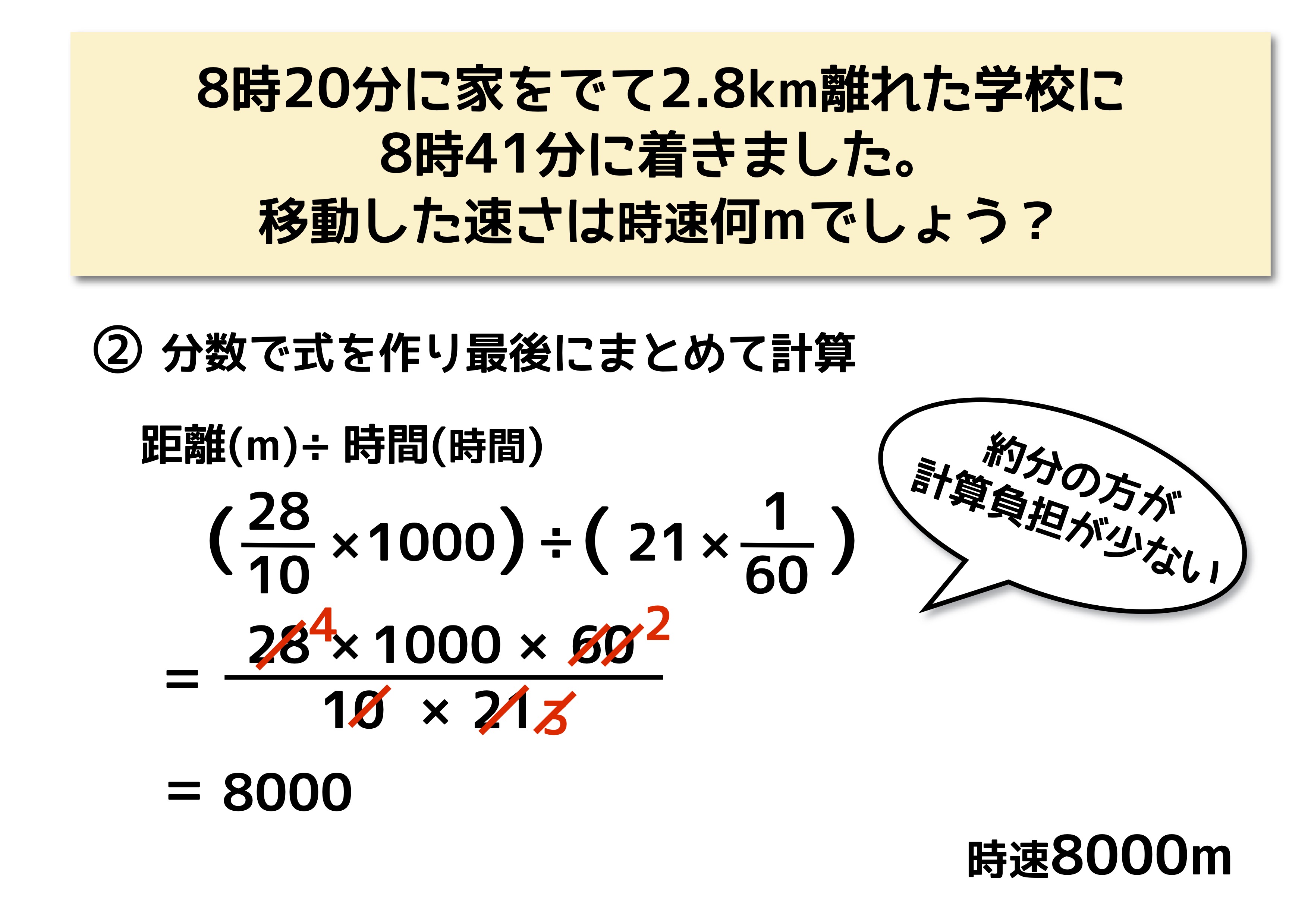
時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく
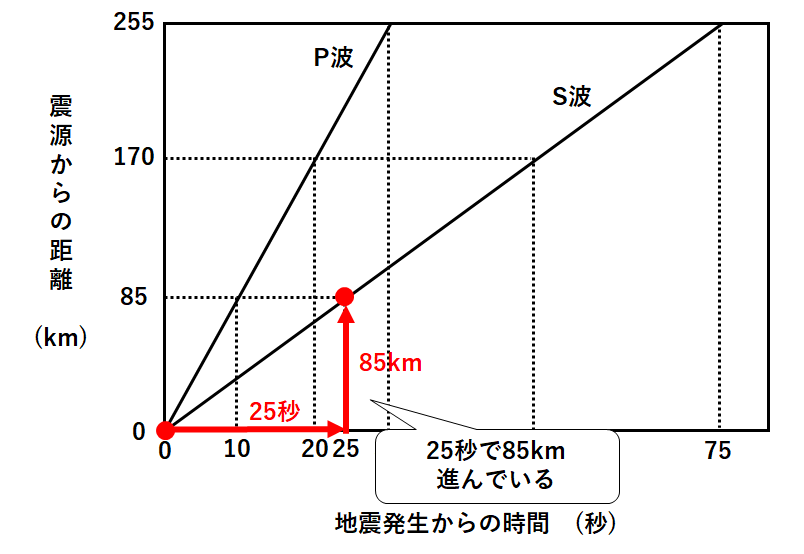



中1地学 地震の計算問題の考え方 中学理科 ポイントまとめと整理




中1数学 文字で表すコツ4 速さ 時間 距離 練習編 映像授業のtry It トライイット




数学 図の解き方例 吉岡進学塾 新居浜市の学習塾 英語や英検対策 数学や算数を教えています
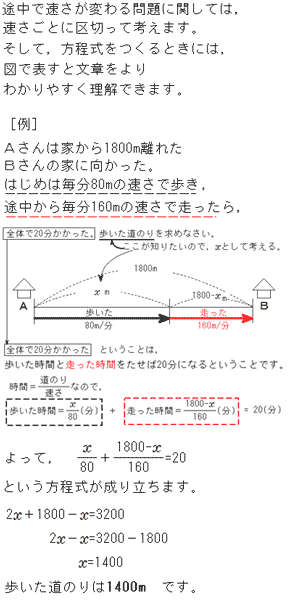



方程式 途中で速さが変わる問題の解き方 中学生からの質問 数学 進研ゼミ中学講座 中ゼミ




数学公式 速さ 時間 道のり 距離 ってなんだろう Qikeru 学びを楽しくわかりやすく




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生
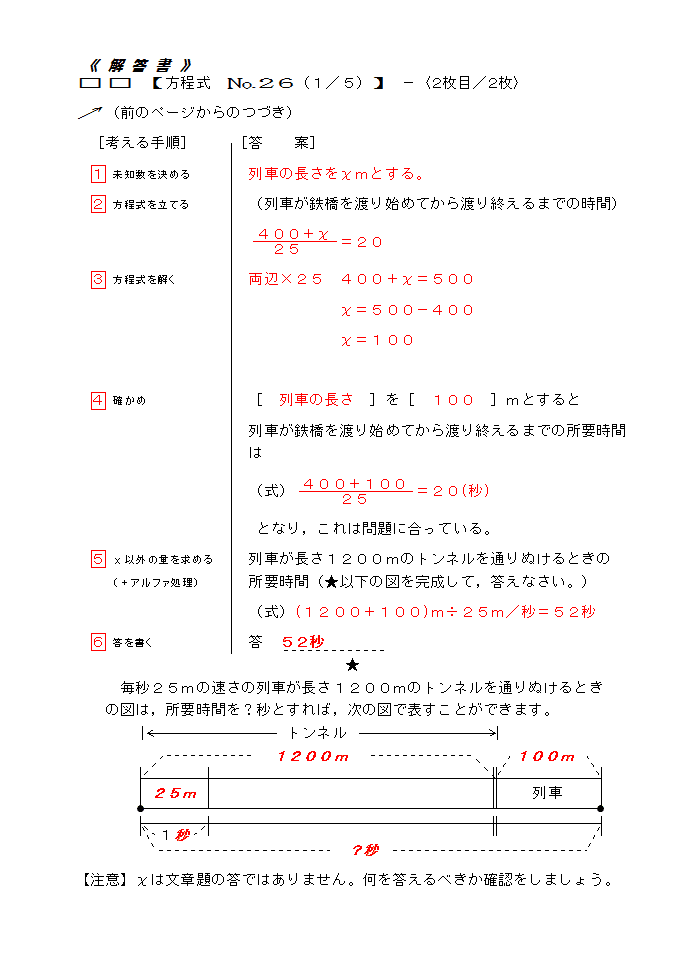



中1数学 方程式 26 1 中学数学高校数学個別指導in山形市 数専ゼミ




途中で速さが変わる速さの問題を解説 面積図を使って簡単解決



連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく



連立方程式 代金と速さの文章問題の解き方 と線分図の利用



最高かつ最も包括的な速さかける時間 最高のぬりえ




0iu73mj6jzuntm



時速の計算が苦手なのは きはじ みはじ はじき に頼っているからだ ねんごたれログ




0mogge1o0xnnfm




地震ー表やグラフなどの計算問題 無料で使える中学学習プリント




基本 一次方程式の利用 速さ なかけんの数学ノート
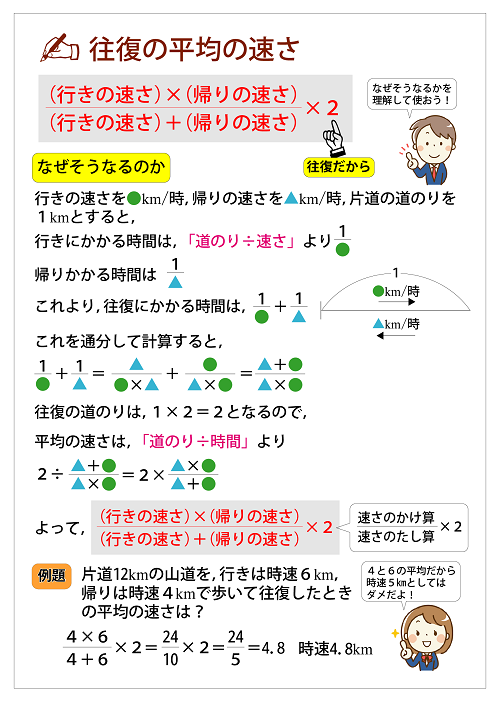



往復の平均の速さに関する公式のカードを作りました 恋する中高一貫校 適性検査 徹底攻略




中3理科 速さの計算方法 Examee



無料 中1数学 基本解説 問題プリント 方程式5 方程式の利用3 127



Q Tbn And9gct96aptzhcl9zdlh2cs6ojaa96y00ldhy9ylcromy3me7fuvx J Usqp Cau



速さ 時間 距離のドリル




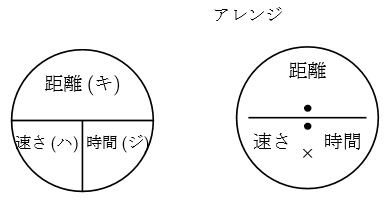
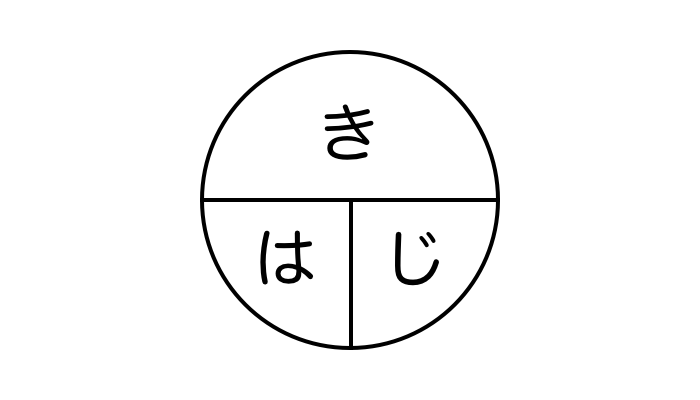
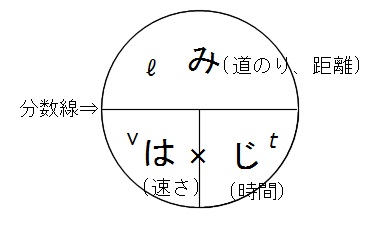
はじき みはじ の法則 速さ 時間 距離 簡単な公式の覚え方 Yattoke 小 中学生の学習サイト おはじき 学習 算数




往復の平均の速さ 間違えずに求められますか



1
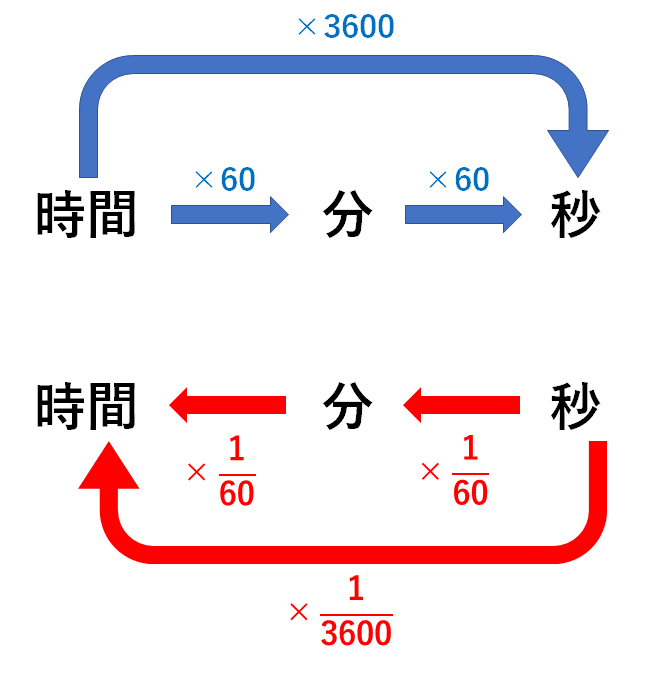



中3物理 速さの単位変換 中学理科 ポイントまとめと整理
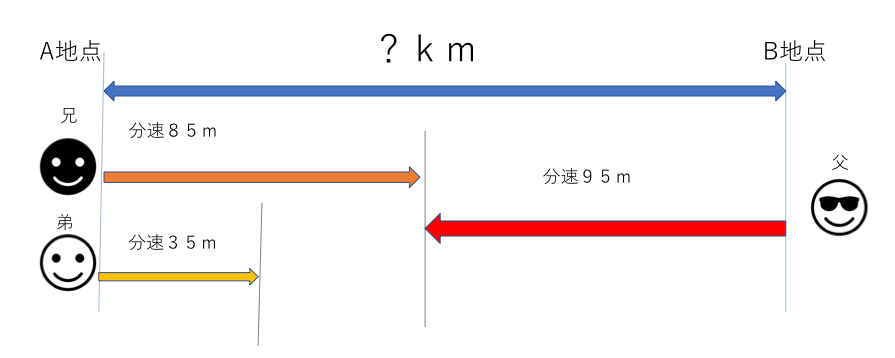



中学受験 算数 速さの重点ポイントまとめ 比を使った裏技公開 中学受験アンサー
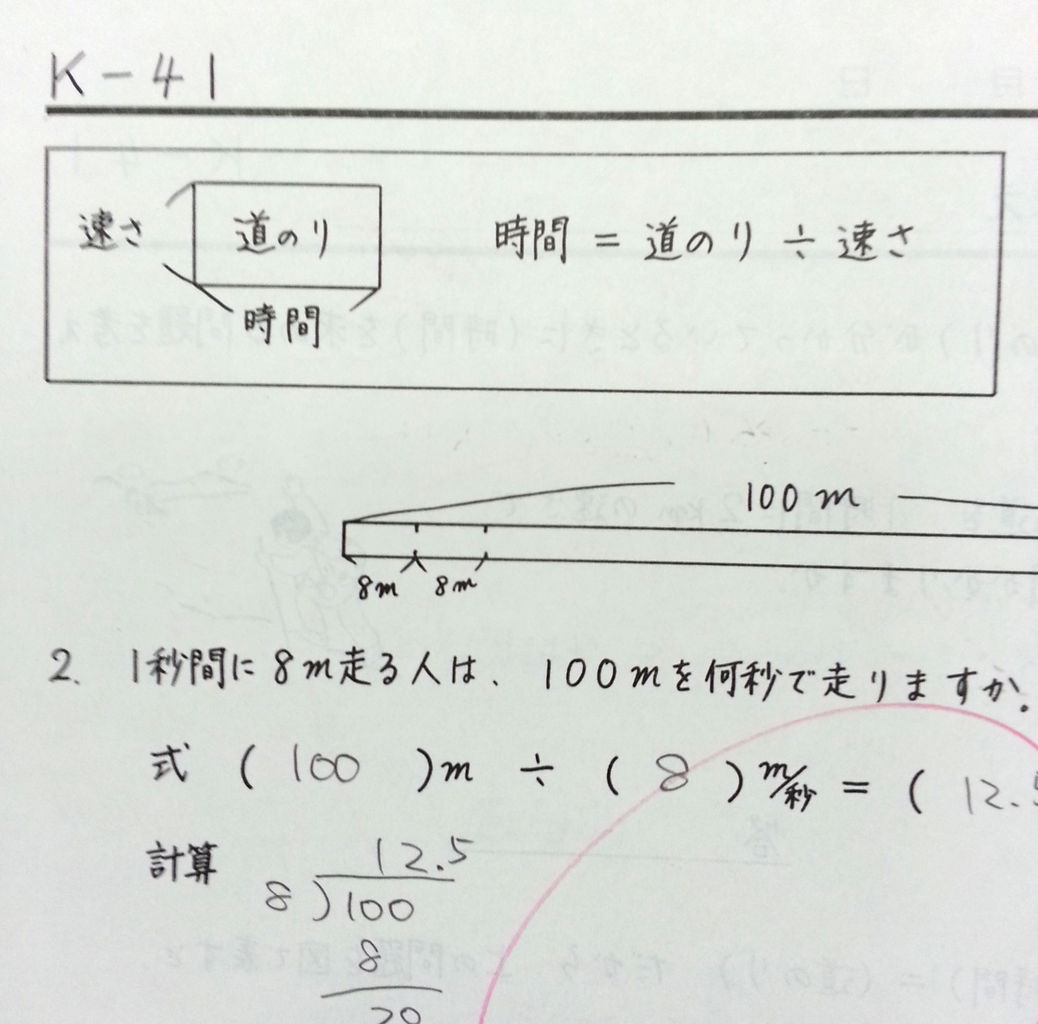



小学生が算数でつまずきやすい 速度 問題を克服 小 中学生向け補習塾 算数 数学 国語 ほめるん By じりつ堂



無料 中1数学 テスト対策問題 問題プリント 118 方程式5 文章題3



小中学生 道のり 速さ 時間の公式を理解しよう 偏差値40プログラマー



中2数学 一次関数の利用 距離 時間 速さ 定期テスト対策予想問題 中学生勉強サイトあかね先生




数と式 一次不等式を扱った応用問題を解いてみよう その3 道のり 速さ 時間 日々是鍛錬 ひびこれたんれん



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋




物体の運動と速さの基本 無料で使える中学学習プリント




の問題なのですが 私は初速度 速度 加速度 時間の公式にあてはめて計算したのですが Clear




はじきの計算 例題を使って問題を解説 速さ 距離 時間を求める方法は 数スタ



速さの問題 中学受験 田中貴 Com



Lh3 Googleusercontent Com Proxy Dcihpydvt5jftwzk9oryktsyjfyxz6xw7sqvyyetezk Iny1 7py74bgiwlo Zxbbqkalb2m Ac3iolq2x X93rynmujw8opc2gkeovjncduc Gn6wzbauxm73vscajvgxc02stg8fnx3zr7dxsydveomfn9npa Tg0dd8iag3mthffjn4nsfc7iqpsyls Kvn7m Kdjvgxfvx0fkh4h5vyv6hz6 Xxoizvy




中1 数学 方程式9 文章題 速さ 17分 Youtube




方程式利用 何分後に追いつくか 速さの文章問題を徹底解説 数スタ




同地点から一定時間 反対方向へ進んで出会うパターン 池の周りを回ってみる 07 21 中学数学の速さ 時間 距離に関する問題 Makelemonadejp Com



時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




音の速さとよくでる計算問題 Sciencenote Jp



中1 一次方程式の文章題 距離 時間 速さ関連の問題 中学数学の方程式 中間 期末テスト 高校入試対策



中1数学 基本 基礎問題 方程式の利用3 文章問題 127




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり



グラフから速さを求める 中学から数学だいすき



中学受験 流水算は 4つ速さを整理すれば簡単に解ける かるび勉強部屋




ボード 双子へ のピン



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり
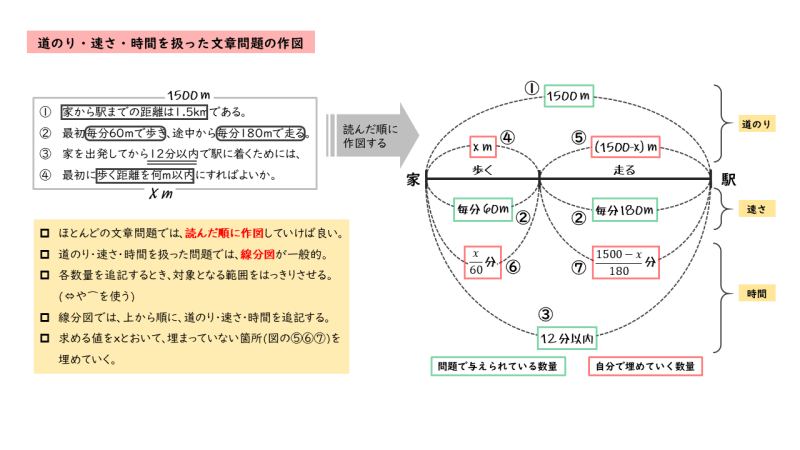



数と式 一次不等式を扱った応用問題を解いてみよう その3 道のり 速さ 時間 日々是鍛錬 ひびこれたんれん




大仏先生 現役大手進学塾数学講師 高校受験 方程式の文章題 速さ 例外はあるが基本的に 時間をxとおくと 距離 について立式 速さ 時間 を使う 距離をxとおくと 時間について立式 速さ 距離 を使う 例は画像参照 高校入試 高校受験 数学



1




往復の平均の速さ 間違えずに求められますか
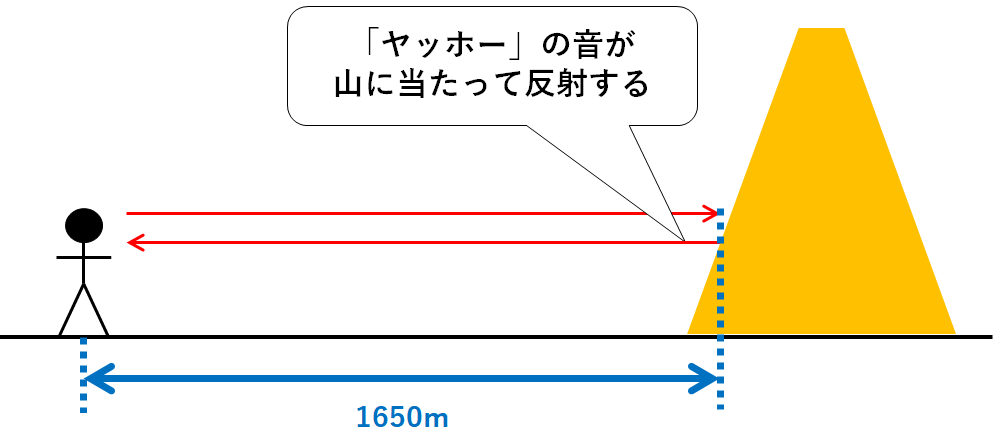



中1物理 音の速さの計算 中学理科 ポイントまとめと整理




旅人算 の問題の解き方 小学生に教えるための分かりやすい解説 数学fun



わかる 中学数学 一次方程式の利用 文章題 道のり 速さ 時間の問題 を丁寧解説




中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




時速や分速の計算でミスをしないために 分数の約分利用の徹底を 中学受験ナビ




中2数学 連立方程式の文章題 速さ 練習編 映像授業のtry It トライイット




速さの問題のみはじ 速さの計算問題は 速さ 道のり 時間 の3つの要素を意識すればよい



音の速さの計算問題をくわしく解説



3




中学2年生数学ー連立方程式 長野地区 Itto個別指導学院 長野市の学習塾




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




小6 算数 小6 21 速さの表し方 基本編 Youtube



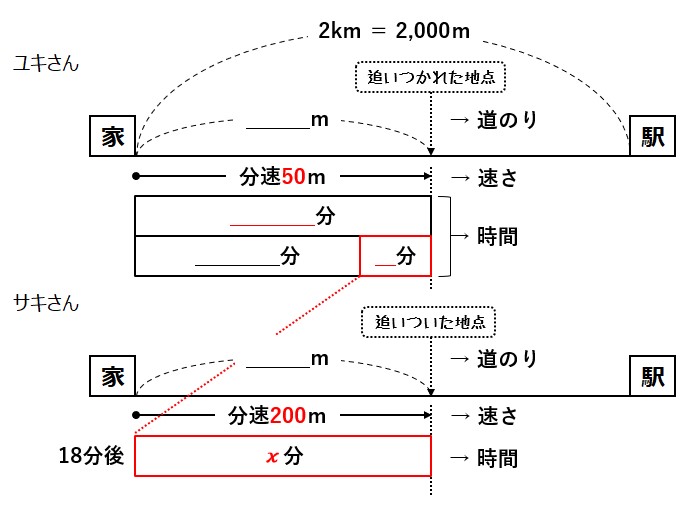
方程式 途中で速さが変わる問題の解き方 中学数学 定期テスト対策サイト




旅人算 中学入試問題をわかりやすくマンガで攻略 マンガで算数シリーズ 3 禎一 樋口 利雄 本間 本 通販 Amazon




中学数学 必見 苦手な文章問題の簡単な解き方のコツ 数学の面白いこと 役に立つことをまとめたサイト




中1数学 方程式の文章題 速さ 練習編 映像授業のtry It トライイット




中1数学 方程式の文章題 速さ 例題編 映像授業のtry It トライイット



中学数学 1次方程式 文章題の解き方 速さ 時間 道のり




速さ 坂道の問題 14 前田昌宏の中学受験が楽しくなる算数塾
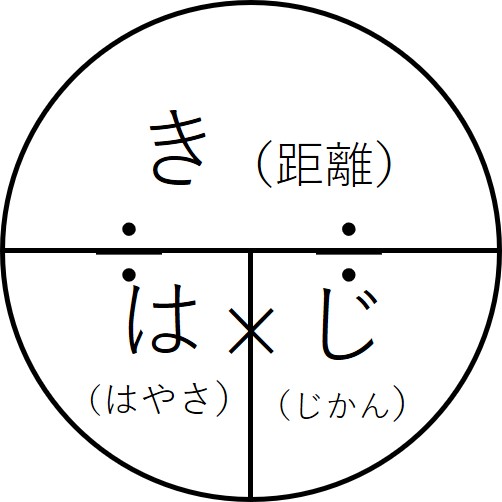



小学生 算数 完全習得 速さの計算 こいがくぼ翼学習塾




物体の運動




等速直線運動 高校物理をあきらめる前に 高校物理をあきらめる前に




小学5年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




小学6年生 速さ 時間 道のり 練習問題プリント ちびむすドリル 小学生




連立方程式 文章題 距離 速さ 時間 中学数学 練習問題プリント 数奇な数
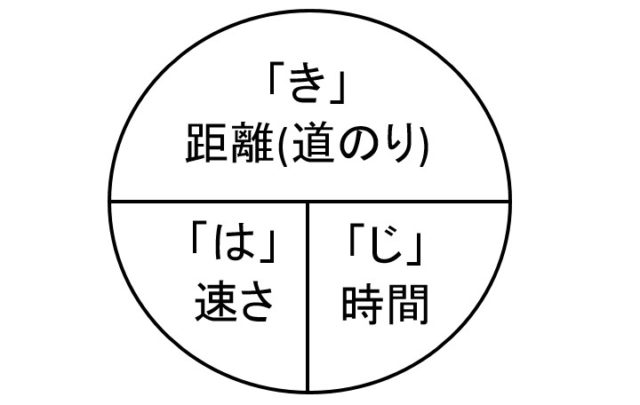



2学期開始 小5の算数は要注意 南茨木教室 You 学舎からのお知らせ




速さ 時間 距離 はじき みはじ の法則 小学生 中学生の無料学習プリント Yattoke プリント カード
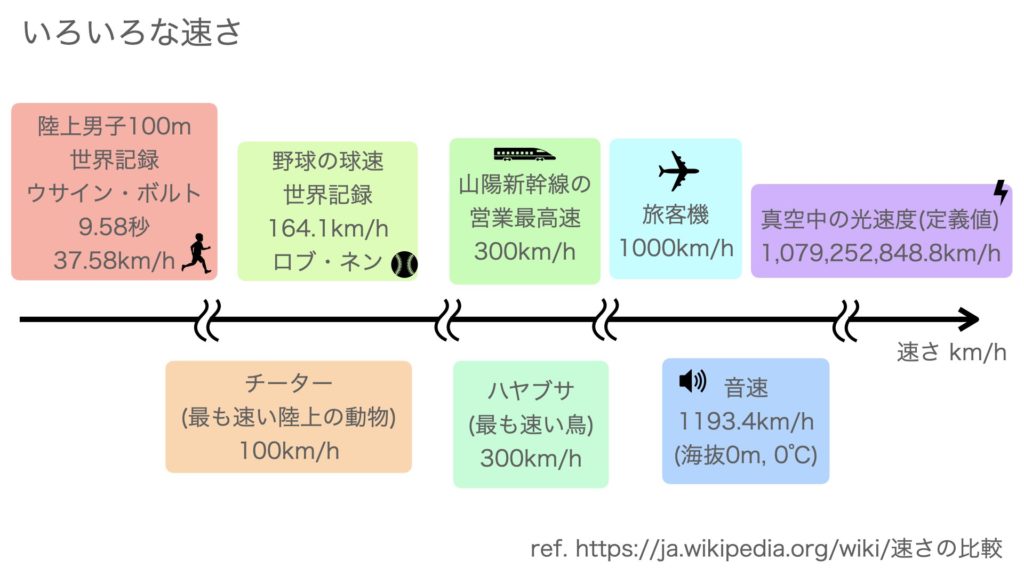



音の速さとよくでる計算問題 Sciencenote Jp



0 件のコメント:
コメントを投稿